Найдите область определения функции:
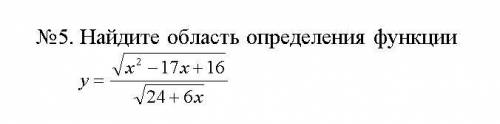
Другие вопросы по теме Алгебра
Популярные вопросы
- если что это дроби семь восьмых минус четыре пятых...
3 - Число увеличили на 5/12 и получили 1736. Какое число увеличили?...
2 - Дана пропорція 2:15=0,4:3 запишіть різницю середніх чисел....
1 - ответьте на вопросы, используя активную лексику урока....
1 - Побудувати трикартинне комплексне креслення відрізку ав прямої...
3 - Перечислите транспортировки утопающего...
1 - решить уравнение 7.24 алгебра...
3 - Проверочная работа по теме «Признаки равенства треугольников» 1)...
2 - No3 «Бәйтеректің» суретін сал. Сөйлем құра....
2 - Верно, что плоскости параллельны, если прямая, лежащая в одной...
2
ответ: D(y) = (-4 ; 1] ∪ [16 ; +∞)
Объяснение:
1) Подкоренные выражения не могут быть меньше ноля.
(1)
Решаем по теореме Виета:
Метод интервалов (см. вложение)
x ∈ (−∞ ; 1] ∪ [16 ; +∞)
(2)
x ∈ [-4 ; +∞)
Делить на ноль нельзя ⇒ знаменатель долен быть больше ноля.
x ∈ (-4 ; +∞)
D(y) = ((−∞ ; 1] ∪ [16 ; +∞)) ∩ [-4 ; +∞) ∩ (-4 ; +∞)
D(y) = (-4 ; 1] ∪ [16 ; +∞)