Найдите область определения функции
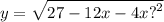
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Мәтінді мұқият оқыңыз және перифразаның түрлі тәсілдерін...
3 - Найдите значения выражения: а) 3/4:5/8 б...
3 - Власне висловлюваня на тему: У різних ситуаціях ми поводимося...
2 - 4. Прослушай стихотворение С. Сейфуллина. Родная земля С тобой...
2 - Choose the phrase to match the right preposition...
3 - Запишите реакции получения кислорода из пернагоната калия и...
1 - Work in pairs or small groups. Look at the photos and these...
1 - Композиція драматичного твору...
2 - Дам 40 скрочно с литературой...
1 - Таблица по повести Нщчь перед Рождеством...
3
В решении.
Объяснение:
Найти область определения функции:
у = √27 - 12х - 4х²;
Область определения функции - это значения х, при которых функция существует.
Подкоренное выражение не может быть отрицательным.
Решить неравенство -4х² - 12х + 27 < 0 и найти НЕДОПУСТИМЫЕ значения х.
-4х² - 12х + 27 < 0
Приравнять к нулю и решить квадратное уравнение:
-4х² - 12х + 27 = 0/-1
4х² + 12х - 27 = 0
D=b²-4ac =144 + 432 = 576 √D=24
х₁=(-b-√D)/2a
х₁=(-12-24)/8
х₁= -36/8
х₁= -4,5;
х₂=(-b+√D)/2a
х₂=(-12+24)/8
х₂=12/8
х₂=1,5.
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, парабола пересекает ось Ох в точках х = -4,5 и х=1,5.
Решение неравенства х∈(-∞; -4,5)∪(1,5; +∞).
Это недопустимые значения х.
Значит, область определения функции в интервале от х= -4,5 до х=1,5.
Запись: D(у) = х∈(-4,5; 1,5).