Найдите область определения: 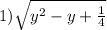
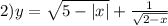
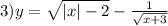
Другие вопросы по теме Алгебра
Популярные вопросы
- Fill in the gaps. dear vera, kate and sam are in indonesia. are photos....
2 - Постройте график функции: у=4/5х+1 у=-4,5х+2 у=0,75-1...
3 - У=3/4х+5. как найти х ,если у =[-4; 4]...
3 - Сочинение на тему моё любимое животное из зоопарка на языке с переводом...
1 - Ширина бруска в 1,4 раза меньше его длины ,а его высота равна 5 дм....
2 - Сегодня в школе 4 урока уроки в школе начинаются с 9 часов каждый урок...
3 - Как добрался до острова робинзон крузо...
1 - Решите уравнение 10-24x=3,16 (y+6,2)*23=70,84...
1 - А) 2а+3а= б) 3х+5х= в)12y-7y= г)7б-4б= д)x-8x= е) а-12а= ж) -б-6б=...
2 - Write the verbs in brackets into the right form: 1. miss grier asked...
3
Объяснение:
1)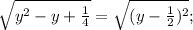
область определения: y∈(-∞;+∞);
2)
x<2
область определения: x∈[-5;2);
3)
x∈(-∞;-2]∪[2;+∞); с другой стороны x>-3;
область определения: x∈(-3;-2]∪[2;+∞);