Найдите неопределенный интеграл

17 и 18 задача, с пошаговым решением

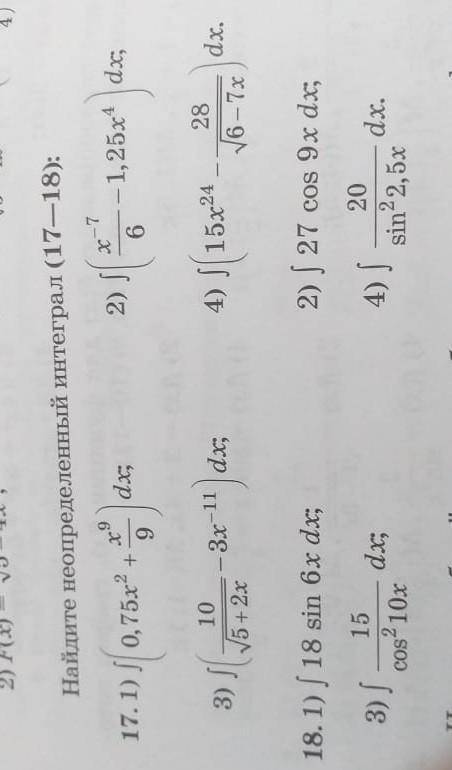
Найдите неопределенный интеграл17 и 18 задача, с пошаговым решением

Ответы

lllJenyalll 15.10.2020 20:29

Найдите неопределенный интеграл:

17. 1)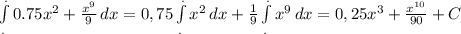 $\int\limits^._. {0.75x^2+\frac{x^9}{9} } \, dx =0,75\int\limits^._. {x^2} \, dx+\frac{1}{9}\int\limits^._. {x^9} \, dx =0,25x^3+\frac{x^{10} }{90} +C$

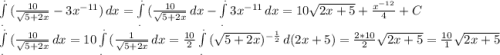3) $\int\limits^._. {(\frac{10}{\sqrt{5+2x} }-3x^{-11} }) \, dx = \int\limits^._. {{(\frac{10}{\sqrt{5+2x} }} \, dx -\int\limits^._. {3x^{-11} }} \, dx =10\sqrt{2x+5}+\frac{x^{-12}}{4}+C\\ \int\limits^._. {{(\frac{10}{\sqrt{5+2x} }} \, dx = 10\int\limits^._. {{(\frac{1}{\sqrt{5+2x} }} \, dx= \frac{10}{2}\int\limits^._. {(\sqrt{5+2x})^{-\frac{1}{2} } } \, d(2x+5) = \frac{2 * 10}{2} \sqrt{2x+5}= \frac{ 10}1{ \sqrt{2x+5}$ 18.

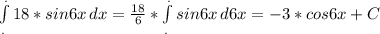
1) $\int\limits^._. {18*sin 6x} \, dx = \frac{18}{6}*\int\limits^._. {sin6x} \, d6x=-3*cos6x +C$

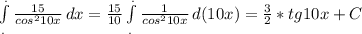
3) $\int\limits^._. {\frac{15}{cos^{2}10x} } \, dx = \frac{15}{10}\int\limits^._. {\frac{1}{cos^{2}10x} } \, d(10x)= \frac{3}{2}*tg10x+ C$

Объяснение: Интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.

P.S. 2 и 4 не решаю, потому что они аналогично решаются.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра