Найдите натуральное число n такое ,что A^2n =10
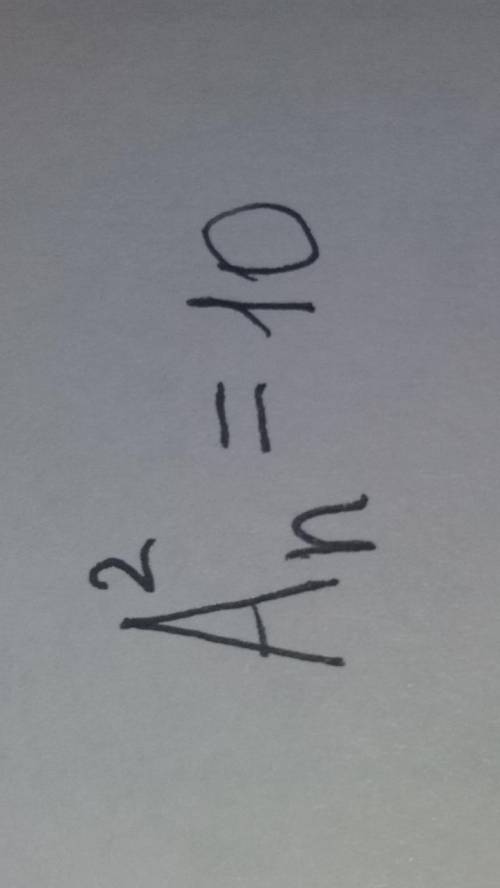
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите наименьшее значение квадратного трехчлена a^2-4a+7...
2 - Составить письмо самому себе в будущее...
2 - Ошироком распространении грамотности на руси свидетельствует большое...
3 - На какой вопрос отвечает слово далеко...
2 - Сколько различных инициалов (фио) можно образовать, используя 6 первых...
1 - На конференцию приехали 865 делегатов. каждый из них говорил по крайне...
3 - Заполни таблицу член предложения что обозначает на какой вопрос отвечает...
1 - Напишите, словосочетание причастия x +существительное и причастие...
3 - Найдите площадь прямоугольной трапеции, у которой меньшее основание...
2 - Составить ! придумать вопросы для хвостиков arent i? can you didnt...
1
Для начала, давайте разберемся с тем, что означает выражение "A^2n". Знак "^" означает возведение в степень, а число n после этого знака указывает, в какую степень нужно возвести число A. В данном случае мы имеем A^2n, что означает, что число A нужно возвести в степень 2n.
Задача состоит в том, чтобы найти такое натуральное число n, при котором A^2n будет равно 10. Давайте разберемся, как это сделать.
Изначально, у нас есть квадратная таблица, в которой в каждой ячейке находится число, подобное тому, что изображено на картинке. Мы видим, что числа в ячейках расположены в порядке возрастания, начиная с 1.
Давайте посмотрим на квадраты некоторых чисел, чтобы найти некоторые закономерности:
A^2 = 1^2 = 1
A^4 = 2^2 = 4
A^6 = 3^2 = 9
A^8 = 4^2 = 16
A^10 = 5^2 = 25
Мы видим, что квадраты чисел увеличиваются в порядке возрастания, начиная с 1 и увеличиваясь на 3 с каждым шагом. Теперь нам нужно найти такое натуральное число n, чтобы A^2n было равно 10.
Исходя из наших наблюдений, мы можем предположить, что число A^2n для A = 3 будет иметь формулу 3^2n и будет равно 9^n. Теперь нам нужно найти такое натуральное число n, при котором 9^n равно 10.
Решим это уравнение методом подбора. Нам нужно найти натуральное число n, при котором 9^n равно 10. Пробуем разные значения для n:
Для n = 1: 9^1 = 9 (не равно 10)
Для n = 2: 9^2 = 81 (не равно 10)
Для n = 3: 9^3 = 729 (не равно 10)
Для n = 4: 9^4 = 6561 (не равно 10)
...
Для n = 9: 9^9 = 387420489 (не равно 10)
Мы видим, что ни одно из этих значений не удовлетворяет условию задачи. Поэтому мы можем сделать вывод, что нет такого натурального числа n, при котором A^2n будет равно 10.
Таким образом, ответ на задачу состоит в том, что не существует натурального числа n, при котором A^2n будет равно 10.