1. Алгебра
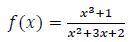
  2. Найдите наклонную асимптоту

Найдите наклонную асимптоту


Найдите наклонную асимптоту

Didi12EW Didi12EW    1   01.01.2022 15:26    1

Ответы
XyJiuGaN4uK XyJiuGaN4uK  01.01.2022 15:30

ответ:   у=1 .

f(x)=\dfrac{x^2+1}{x^2+3x+2}  

Наклонная асимптота - это прямая вида  y=kx+b . Найдём k и b по известным формулам .

k=\lim\limits_{x \to \infty}\, \dfrac{f(x)}{x}=\lim\limits_{x \to \infty}\, \dfrac{x^2+1}{x\, (x^2+3x+2)}=\lim\limits_{x \to \infty}\, \dfrac{x^2+1}{x^3+3x^2+2x}=\lim\limits_{x \to \infty}\, \dfrac{x^2}{x^3}=0b=\lim\limits_{x \to \infty}\, (f(x)-kx)=\lim\limits_{x \to \infty}\, \dfrac{x^2+1}{x^2+3x+2}=\lim\limits_{x \to \infty}\, \dfrac{x^2}{x^2}=1

Уравнение наклонной асимптоты: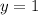   y=1  . Получили частный случай, когда наклонная асимптота становится горизонтальной асимптотой .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Verabogomaz Verabogomaz  18.11.2020 08:30
20.7. Задайте функцию таблицей с формулы у = х2, если область определения этой функции состоит из чисел:1) -3; -2; -1; 0; 1; 2; 3;2) -30; -20; -10; 0; 10; 20; 30;3)...
frost09042004ozo97y frost09042004ozo97y  18.11.2020 08:31
При каких значениях b уравнение 2у^2-by+7=0 имеет два равных корня?...
Соня8912 Соня8912  18.11.2020 08:31
Алгебра 10сынып 19.3 есеп 19.8 осы есеп стем бериндериндерш по братски пажы...
Slonik3452 Slonik3452  18.11.2020 08:31
Определите при каких значениях переменной √(1+8х) выражение не имеет смысла. ​...
Nastya165567 Nastya165567  18.11.2020 08:32
Вынесите множитель из-под корня....
coldenye coldenye  18.11.2020 08:33
ХЕЛПМИ , ОМГ я тупая(T^T)Решите только 1, 3, 5, 7​...
ДаняКашин ДаняКашин  18.11.2020 08:42
Найти значения выражения :при x = - 3 5х+2-(-3+6х)-х= Номер 2 упростить : (3х-5у)-4(х-6у)= 4х-(3х+(5х-2))=...
arlanout arlanout  09.04.2019 10:43
Найдите все с при которых уравнение х в квадрате + сх +1,5с=0 имеет два карея​...
elizaveta08071999 elizaveta08071999  09.04.2019 10:44
Нужна ваша буду сильно признателен если сделаете хоть 3,с решением,заранее...
dymomc dymomc  09.04.2019 10:45
2, 5. 5. 10. найдите 9 член прогрессии.​...

Популярные вопросы