1. Алгебра
  2. Найдите наименьшее значения

Найдите наименьшее значения функции у= х^4 на отрезке [-1;2]

366023 366023    1   06.10.2020 09:07    2

Ответы
mokeevayulichk48 mokeevayulichk48  06.10.2020 10:01

0

Объяснение:

Найдём экстремумы функции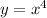 y= x^4:

Найдем производную: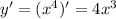 y'=(x^4)'=4x^3

Найдем корни уравнения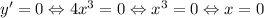 y'=0\Leftrightarrow4x^3=0\Leftrightarrow x^3=0 \Leftrightarrow x=0

То есть в точке 0 функция имеет глобальный минимум.

Так как функция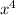 x^4 в точке 0 имеет глобальный минимум:

\displaystyle\min_\mathbb{R}(x^4)=0, а точка 0 находится между точками -1 и 2, то \displaystyle\min_\mathbb{R}(x^4)=\min_{[-1;2)}(x^4)=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
MrKreeD1 MrKreeD1  04.06.2019 12:30
Вычислить cosa tga ctga если sina=-(4/5) и п...
Ульяна1561 Ульяна1561  04.06.2019 12:30
Варифметической прогрессии сумма первого и шестого члена равна 11, а сумма второго и четвертого членов равна 10. найти сумму первых 6 членов этой прогрессии...
zarrrubinka zarrrubinka  15.10.2020 20:20
ПОСОГИТЕ между какими соседними натуральными числами заключено числоа) √38 в) √17-2?​...
lololo20021 lololo20021  15.10.2020 20:21
народ кто сделает в профиле лукос поставлю...
kudar2 kudar2  15.10.2020 20:28
На первой тарелке лежит в 4 раз меньше слив, чем на второй. Если бы со второй тарелки переложила на первую 6 слив, то из на тарелка стало бы поровну. Сколько слив лежит на каждой...
leo1233121 leo1233121  15.10.2020 20:35
плз ребят оч надо кр оттдаю все что есть...
azmamatovm azmamatovm  15.10.2020 20:36
0,5m×2x =otvetbpomogite pojaluista...
иоапгрдгоп иоапгрдгоп  27.08.2019 20:40
2x/2-x+5 больше0 x/2-1,5x-11 больше или равно 0...
Мерконюк Мерконюк  27.08.2019 20:40
36(6х+1)=9(4-2х) 3,2(3х-2)=-4,8(6-2х)...
alinamensikova alinamensikova  27.08.2019 20:40
График какого уравнения не проходит через точку (-3; 1) а)2х+3у=-3 б)2х-у=-7 в)2х+9у=3 г)2х-3у=9...

Популярные вопросы