1. Алгебра
  2. Найдите наименьшее значение выражения

Найдите наименьшее значение выражения

Саша12811 Саша12811    2   25.04.2022 17:42    2

Ответы
IncolaRO IncolaRO  25.04.2022 17:50

ответ:   2 .

Объяснение:

   Перетворимо даний триг. вираз ( ctgα - tgα )/( cos4α + 1 ) =

= ( cosα/sinα - sinα/cosα )/( 2cos²2α ) = ( cos²α -

- sin²α ) / ( sinαcosα2cos²2α ) = 1/( sin2α cos2α  ) = 2/(2sin2α cos2α ) =

= 2/sin4α .   Вираз    2/sin4α  , який дорівнює даному , має найменше

значення  , коли його знаменник має найбільше значення sin4α = 1 ;

воно досягається при  α = π/8 Є ( 0 ; π/4 ) . Найменше значення

даного виразу буде дорівнювати  2 : 1 = 2 .

ПОКАЗАТЬ ОТВЕТЫ
F1kser F1kser  25.04.2022 17:50

ответ: 2

Объяснение:

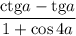
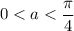
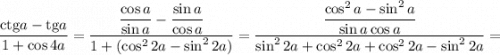
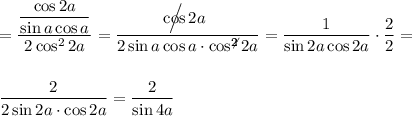
Найдите наименьшее значение выражения

\displaystyle \frac{\mathrm {ctg}a - \mathrm{tg }a}{1+ \cos 4a}

при   0 < a < \dfrac{\pi }{4}
 
\displaystyle \frac{\mathrm {ctg}a - \mathrm{tg }a}{1+ \cos 4a} = \frac{\dfrac{\cos a}{\sin a} - \dfrac{\sin a }{\cos a} }{1 + (\cos^22a - \sin^2 2a )} = \frac{\dfrac{\cos^2 a - \sin ^2 a}{\sin a\cos a} }{\sin ^22 a + \cos ^22a+ \cos^22a-\sin^22a} =

\displaystyle=\frac{\dfrac{\cos 2a }{\sin a\cos a} }{2\cos ^22a} = \frac{ \Big\slash \!\!\!\!\!\!\!\!\cos 2a}{2\sin a\cos a\cdot \cos^{ 2\!\!\!\not 2} 2a } = \frac{1}{\sin 2a \cos 2a}\cdot \frac{2}{2} = \frac{2}{2 \sin 2a\cdot \cos 2a} = \frac{2}{\sin 4a }

0 < 4a < \pi

Так как в данных четвертях синус положительный , то для того  чтобы получить наименьшее  значение  знаменатель должен быть максимальным  sin4a = 1


\dfrac{2}{\sin 4a } =\dfrac{2}{\sin 90} = 2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ifrut52 ifrut52  14.07.2019 12:10
Выражение и найдите его значения при указанном значении переменной: 1) (2а-1)³-8а³+при а=-2 2) (0,5b-2)³-(0,5b+2)³ при b =-2 3) (3х-4)³+(3х-2)³-27х³ при х=0,5 4)(0,2+5у)³-(0,5+2у)³-6у²при...
darinaprokopenk darinaprokopenk  14.07.2019 12:10
Решите уравнение 1) (x+1)^3-(x-1)^3=x(6x+2) 2)(x+2)^3-(x-1)^3=9x^2+36 3)(x-2)^3-3x^2-4=(x-3)^3 4)(x+3)^3=x^2(x+9)...
SuperGirl1111468 SuperGirl1111468  14.07.2019 12:10
Решите уравнение 1) (x+1)^3-(x-1)^3=x(6x+2) (2)(x+2)^3-(x-1)^3=9x^2+36 (3)(x-2)^3-3x^2-4=(x-3)^3 (4)(x+3)^3=x^2(x+9)...
Pollymironova Pollymironova  13.09.2019 21:50
Выражение 2(0,3х + 1) – 0,4(3х + 5) и вычислите его значение при x5/6...
ashbringer12332 ashbringer12332  13.09.2019 21:50
Преобразуйте в многочлен стандартного вида выражение (x-1)(x+5)...
olena4519 olena4519  07.08.2019 10:20
Три гнома съели все запасы конфет. первый гном съел 100 гр конфет и одну третью часть оставшихся конфет. второй гном съел 200 гр конфет и половину оставшихся конфет....
Кирилл6901 Кирилл6901  07.08.2019 10:20
Требуется перевезти 76 тонн груза на автомобиле,грузоподьемность которого равна 6 тоннам.какое минимальное число рейсов придется сделать? решение...
alinamazur003 alinamazur003  07.08.2019 10:20
Нужна ! решить квадратное неравенство: 1)-6х²-х+12 0 2)-3х²-6х+45 0...
furymalice furymalice  07.08.2019 10:20
Решить квадратное неравенство: 1)-2,1х²+10,5х 0 2)-3,6х²-7,2х 0...
динозаурус динозаурус  07.08.2019 10:20
Воздоровительный лагерь готовились отправить 360 кг картошки на 135 человек одной смены. но стало известно, что в лагере будет 120 человек. сколько килограмм картошки...

Популярные вопросы