1. Алгебра
  2. Найдите наименьшее значение функции:

Найдите наименьшее значение функции: y=3^(x^2-6x+14)

никита154856 никита154856    1   31.07.2019 04:10    0

Ответы
Бебка228 Бебка228  28.09.2020 11:46

y наиб = 243

Объяснение:

Дана функция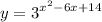 y={\displaystyle 3^{x^{2}-6x+14} }

Производная функции

y'={\displaystyle 3^{x^{2}-6x+14} \cdot ln3 \cdot (2x - 6) }

y' = 0

{\displaystyle 3^{x^{2}-6x+14} 0}

ln3 > 0

2x - 6 = 0

x = 3

При х < 3 y' < 0, следовательно, функция у↓ (убывает)

При х > 3 y' > 0, следовательно, функция у↑ (возрастает)

Это значит, что х = 3 - точка минимума

\displaystyle{ y_{min} = 3^{3^{2}-6 \cdot 3+14}= 3^{5}=243 }

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
dasha1933 dasha1933  17.08.2019 04:20
Выполните умножение многочленов : ( а + 2в ) ( а - 2в ) ( а2 + 4в2 )...
CBeTouD CBeTouD  17.08.2019 04:20
При каком значении х, у равен 0 в уравнении у= 3х^2 + 6х - 9...
Xtanev Xtanev  17.08.2019 04:20
Найдите sin a , если cos a = √7÷4 и а э ( 0; 0,5 )...
amanamisa1 amanamisa1  17.08.2019 04:20
(х+4у)(4х-х) преобразуйте в многочлен стандартного вида...
sssooonnnyyyaaa1 sssooonnnyyyaaa1  17.08.2019 04:20
Дана функция у=f(x), где f(x)=-6x^2. найдите f(1/2a + 2), 2f(x^2 - 1)...
п152 п152  17.08.2019 04:20
Сократить дробь a^2+2a+1/a^-1 и найти ее значения при a=-0,5...
moseva2399 moseva2399  17.08.2019 04:20
Мальчик от дома по направлению на восток 1500м затем вернулся на юг и м на каком расстоянии в местрах оказался мальчик?...
kennysussus kennysussus  17.08.2019 04:20
Избавиться от иррациональности в знаменателе; а) 2/корень из5 б)2/корень из7 -1 решить!...
Viper397 Viper397  17.08.2019 04:20
Надо решить графическим уравнением х в третьей степени=-х-10...
Amalik0 Amalik0  17.08.2019 04:20
Научите мне как решить арифметическую прогрессию десятый п-й член объясните мне...

Популярные вопросы