1. Алгебра
  2. Найдите наименьшее значение функции

Найдите наименьшее значение функции y=2^x^2+2x+5

SashaRary SashaRary    3   28.06.2019 22:40    0

Ответы
лера25jd лера25jd  22.07.2020 23:18

16

Объяснение:

y=2^{x^{2}+2x+5 } =2^{x^{2}+2x+1+4 }=2^{(x+1)^{2} +4} =2^{(x+1)^{2} } *2^{4} =16*2^{(x+1)^{2} } .\\

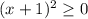Так как (x+1) ^{2}\geq 0 при любых значениях  x , то этот квадрат принимает наименьшее значение 0.  Функция 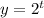y=2^{t} возрастающая . Значит выражение  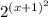2^{(x+1)^{2} } принимает наименьшее значение 1.

И тогда наименьшее значение выражения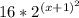     16*2^{(x+1) ^{2} } , а значит и исходного  равно 16.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
shidiemmacom1 shidiemmacom1  14.12.2020 18:04
Постройте график функции 1) y = cos (-x) 2) y = 2cosx 3) y = | cosx | 4) y = tg (x-Пи / 4)...
danilsmetanov6 danilsmetanov6  14.12.2020 18:05
1) √3x+1-√x+4=12)√x-7+3=√5-xнабор возможных значений​...
torgor2017 torgor2017  14.12.2020 18:05
функция заданна формулой y=2x+2 определить: а) значение y если x =0,5 б) значение x при которором y=2 в)проходит ли график функции через точку a(-5;44)...
nastyagosteva nastyagosteva  30.08.2019 17:10
Представьте в виде произведения: 9x^2-4y^2 x^2+8x+16...
5ти 5ти  30.08.2019 17:10
При каких значениях a пара чисел (-2; -1) является решением уравнения ax-2y=-4...
malinkarinka599 malinkarinka599  30.08.2019 17:10
Выполните действия 1)5x(x^2+2x-3) 2)7x(x+y)-7x^2 найдите значение выражения 4а(3a-7)-6a(2a-1) при a=-10...
KristinaLando KristinaLando  30.08.2019 17:10
Решите квадратное уравнение: 3х2 +4,5х = 0...
изу197 изу197  30.08.2019 17:10
Вычислите площадь фигуры ограниченной линиями y=x^4-1 y=1-x^4...
nikadidok nikadidok  30.08.2019 17:10
Выражение (2x+5) (3x-7)+(2x-1) (2x+1)...
инкогнито13131913 инкогнито13131913  03.08.2019 21:10
Один из углов равнобедр трапеции = 138 гр. найти все углы...

Популярные вопросы