Найдите наименьшее значение функции 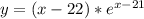на отрезке {20;22}. Если можно подробнее

у наим = у min = -1

Объяснение:

Функция

Производная функции

Найдём точки экстремумов

у' = 0

Известно, что при х ∈ (-∞; +∞)

x - 21 = 0

x = 21

В этой точке производная меняет знак с (-) на (+), следовательно, это точка минимума. Поскольку х = 21 ∈ {20; 22}. то в этой точке данного интервала функция имеет наименьшее значение. Вычислим это значение.