1. Алгебра
  2. Найдите наименьшее значение

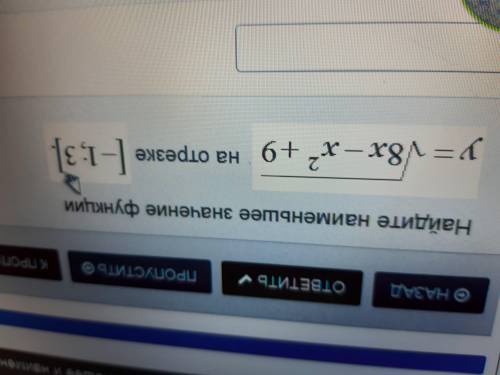
Найдите наименьшее значение функции


Найдите наименьшее значение функции

lovivirus1234 lovivirus1234    3   11.08.2020 16:35    1

Ответы
ден1025 ден1025  15.10.2020 15:51

ответ:0

Объяснение:

Заметим, что y(-1) = √(-8-1+9) = 0

Поскольку радикал неотрицателен, то 0 его наименьшее значение.

ПОКАЗАТЬ ОТВЕТЫ
yulia24082 yulia24082  15.10.2020 15:51

f(x) = \sqrt{8x-x^2+9} = \sqrt{-(x^2-8x)+9)} = \sqrt{(-x^2 - 8x + 16-16)+9} = \sqrt{-(x^2 - 8x + 16) + 9 +16} = \sqrt{-(x-4)^2 + 25} = \sqrt{25-(x-4)^2}

Функция возрастает до x = 4, а после убывает. Значит, минимум соответствует точке x = -1 =>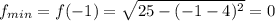 f_{min} = f(-1) = \sqrt{25 - (-1-4)^2} = 0

ответ: 0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
  24.12.2020 21:30
у меня завтра кр, а я ничего не понимаю в теме разложение выражения на множители . Вот пример : 2x(3x-5) +17(5-3x) ...​...
GanifaGasanova505 GanifaGasanova505  24.12.2020 21:30
Решение уравнений. Урок 1 Cколько решений имеет уравнение |x2 + 4x + 6| – 2 = 0?имеет одно решениеимеет четыре решенияне имеет решенийимеет два решенияНазадПроверить​...
ттсссс ттсссс  24.12.2020 21:29
1.Построить график функции. а)y=7x-2б)y=x^2-x-1в)y = \sqrt{x} - 5y=x​−5y = \sqrt{x - 1}y=x−1​2.Исследовать четность нечетность.y=x^3 sin x^23.Исследовать функцию на возрастание...
Дурашка008 Дурашка008  24.12.2020 21:29
Выполните умножение 4x3(ax2+a3x-2a)...
mashka2511 mashka2511  24.12.2020 21:28
Вычислить площадь фигуры, ограниченной линиями: y=-x^2+2x+3 и y=0...
koop2 koop2  11.09.2019 12:20
3умножить на корень из трёх. я провильно понимаю, что получится 27? я не совсе м понимаю принцип действия...
Samlina Samlina  11.09.2019 12:20
Решите уравнение а) 3(0,9x-+0.6)=-0,2 б)7-(3,1-0,1y)=-0,2y...
viktorialychykowtuu4 viktorialychykowtuu4  11.09.2019 12:20
9класс решите уранение с параметром x^2-6a=a^2+6x...
vladyakovlev22 vladyakovlev22  11.09.2019 12:20
Водном ящике в 3 раза меньше конфет,чем во втором ящике.когда из большого ящика пересыпали в меньший ящик 7кг конфе,конфет в обоих ящиках стало поровну.сколько конфет было первоночально...
xAlonerx xAlonerx  19.01.2020 14:46
Вгороде живут 3 миллиона человек. среди них 20% детей и подростков. среди взрослых 75% работает. сколько взрослых жителей работает?...

Популярные вопросы