Найдите наименьшее решение уравнения 11^(x^2-4x-5)=6^(x^2-4x-5)
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите синквейн Санкюлоты12345...
2 - Суміш гліцерину з одноатомним насиченим спиртом масою 14,3 г реагує...
1 - Поставте в кінці речень потрібні розділові знаки. 1. О рідне слово,...
2 - СОР ПО ВСЕМИРНОЙ ИСТОРИИ ОТВЕТЬТЕ НОРМАЛЬНО...
2 - Ақтамберді Сарыұлы «Күлдір-күлдір кісінетіп» толғауындағы жыраудың...
1 - Аяз би ертегісендегі халық құндылықтары эссе 60 сөз...
2 - Придумайте двухстишье на слово творог , квартал, ворота и километр...
3 - Напишите сбалансированные уравнения возможных реакций в молекулярном,...
3 - Решите квадратное неравенство (58–62): 58. 1) х - 3x + 2 = 0;2) х2...
2 - 1. Запишіть дієслова за особами: 1) перша особа; 2) друга особа;...
3
Используемые свойства:
1)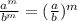
2)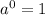
ответ: -1