Найдите наименьшее натуральное число n такое, что среди чисел от n до n + 40403 (включительно) нет ни одного точного квадрата.

Разница квадратов - число нечётное. Даже больше -- разница между квадратами увеличивается на 2:

Т.е наша задача найти такой , что разница между его квадратом и квадратом следующего числа была больше 40403, т.е. 40405. Тогда 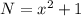(так как включая границы).