1. Алгебра
  2. Найдите наибольшее значение функции

Найдите наибольшее значение функции y=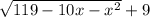\sqrt{119-10x-x^{2} } +9

Roma200511111gnh Roma200511111gnh    3   12.08.2020 20:03    0

Ответы
yliya302 yliya302  15.10.2020 15:53

ответ:21

Объяснение:

Наибольшее значение функции достигается при наибольшем значении квадратного трехчлена, графиком которого является парабола с ветвями вниз. Её наибольшее значение находится при вершине, найдем её координаты:

x_0=\dfrac{10}{-2}=-5\\\max y=y(-5)=\sqrt{119+50-25}+9=\sqrt{144}+9=12+9=21

ПОКАЗАТЬ ОТВЕТЫ
fizaliya1992 fizaliya1992  15.10.2020 15:53

y = \sqrt{119-10x-x^{2} } +9

Заметим что у квадратной функции f(x)= 119 - 10x - x^2 ветви параболы наклонены вниз(т.к -x^2), то есть наибольшее значение данной функции достигается в ее вершины, найдем ее по формуле -b/2a :

x0 = \frac{-(-10)}{2*(-1)} =\frac{10}{-2} =-5

Подставим данное значение в функцию :

f(-5) = 119 -10 *(-5) -(-5)^{2} =119+50-25 = 119+25 = 144

То есть наибольшее значение функции 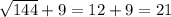 = \sqrt{144} +9 = 12+9 = 21

ответ : 21

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ChristenChy ChristenChy  20.04.2021 18:54
решить Найти промежутки выпуклости и точки перегиба. f(x)=x³-6x²+2x-6...
Kloloko Kloloko  20.04.2021 18:53
Автомобіль мав проїхати 325 км. Проїхавши цієї відстані, автомобіль зменшив свою швидкість на 15 км/год Знайдіть швидкість автомобіля на кожній ділянці руху якщо на весь шлях було...
сдаддае сдаддае  20.04.2021 18:53
чему равно второе уравнение...
д2и0а0н6а д2и0а0н6а  20.04.2021 18:53
знайдіть кількість членів геометричної прогресії ,перший,другий та останній члени якої відповідно допівнюють 5;20 і 5120.....
Matimatichka Matimatichka  20.04.2021 18:52
Упростите: а) (x-y) (x+y) (x²+y²) б) (2a+b)(4a²+b²)(2a-b)в) (c³+b) (c³-b) ( С в 6 степени+b²) г) (3m-2)(3m+2)+4д) 25n²-(7+5n)(7-5n)е) 6x²-(x-0,5)(x+0,5)​...
askardaurenuly askardaurenuly  16.06.2019 20:30
Является ли множество аликвотных дробей замкнутым относительно операции а) сложение б) умножения ? замечание; аликвотными называются дроби с числителем 1...
amozgaleva96 amozgaleva96  16.06.2019 20:30
Верно ли утверждение. что каждое чётно число может быть предоставленно в виде : 2-2m, где m∈z ? решить...
900901 900901  16.06.2019 20:30
Двое рабочих изготовили вместе 108 деталей. первый рабочий работал 5ч, а второй 3ч. сколько деталей изготавливал ежечасно каждый рабочий, если вместе за 1ч они изготавливают 26...
maxkov555p0chlb maxkov555p0chlb  16.06.2019 20:30
Решить уравнение 3x+2y=48. и 3-2y=0...
sofia20015 sofia20015  29.04.2020 18:38
1 Найти значение выражения 3 :(−9 +0,58 16 ) 2 У выражение х3∙(х2)2 3 Разложите на множители: 5у2 – 15у 4 Выполните умножение : (х+6)(х-5) 5 Разложите на множители: 64 – а4с4 2...

Популярные вопросы