1. Алгебра
  2. Найдите наибольшее и наименьшее

Найдите наибольшее и наименьшее значения функций y=x^2+1 на отрезке [0 , 2] 2) найдите наименьшее значение функций f(x)=3sin²x+2cos²x 3)найдите число целых значений x на промежутке убывания функций f(x)=16x³-24x²+9x-1 4)найдите наибольшее и наименьшее значения функций f(x)=√3x + sin 2x на отрезке [0,π/2] в корне только 3х и всё )) решите сколько смошите

Fkrfi134F Fkrfi134F    3   19.05.2019 22:10    0

Ответы
45667889 45667889  13.06.2020 04:46

1)\ y'=(x^2+1)'=2x \\ y'=0 \\ 2x=0 \\ x=0 \\ y(0)=0^2+1=1 \\ y(2)=2^2+1=5

 

ответ:
Наименьшее 1
Наибольшее 5

 

2)\ f(x)=3sin^2x+2cos^2x=3sin^2x+2(1-sin^2x)=sin^2x+2

 

Наименьшее значение выражения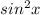 sin^2x это ноль, то есть наименьшее значение функции 2

ответ: 2

 

3)\ f'(x)=(16x^3-24x^2+9x-1)'=48x^2-48x+9 \\ f'(x)=0 \\ 16x^2-16x+3=0 \\ D=256-4*16*3=64=8^2 \\ x_1=\frac{16+8}{2*16}=\frac34\ \ \ \ \ \ \ \ \ x_2=\frac{16-8}{2*16}=\frac14 \\ \\ f'(0)=90\ \ \ \ \ \ \ \ f'(\frac12)=12-24+9=-3<0 \\ \\ f'(1)=48-48+9=90

 

Функция убывает на промежутке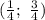 (\frac14;\ \frac34) 

но между этими числами нет целых чисел.
ответ: 0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
KRMP037 KRMP037  22.04.2020 14:59
Найди значение переменной x, если...
zeleninalina20 zeleninalina20  22.04.2020 14:59
-(2/x-2)=2x решите уравнение...
babikahenjudzao babikahenjudzao  22.04.2020 14:59
Как Эрхард развил идею социально рыночного хозяйства?ОТВЕТ НУЖЕН КАК МОЖНО БЫСТРЕЕ...
Paris99 Paris99  22.04.2020 14:59
При каких значениях x выражение имеет смысл log3(x2 - 16)...
софия731 софия731  22.04.2020 14:59
Укажите линейное уравнение с двумя переменными 8/x+3/y=1/7...
pofessorZnanija pofessorZnanija  22.04.2020 14:59
1.Как называется график функции y=kx?2.Через точку с какими координатами проходят все графики функции y=kx, независимо от k?3.В каких четвертях расположен график функции y=kx,...
imverypanda228 imverypanda228  22.04.2020 14:59
Найди значение выражения 19⋅b−45⋅a+19⋅b2b, если a=28, b=84....
Erika211 Erika211  28.04.2020 11:19
У выражение и найдите его значение при x= -2 ( x^3+ 125) - x (x^2+ 3)...
Unicorn5679 Unicorn5679  28.04.2020 11:27
Выразите переменную y через переменную x из уравнения -6у +3х = 24 a) y=4-0,5x б) y=-4-0,5x в) y=-4+0,5x...
bobbobbobgy1 bobbobbobgy1  28.04.2020 11:27
Основание равнобреднного треугольника на 7 см больше его боковой стороны.Найдите боковую сторону треугольника если его периметр равен 43 см.​...

Популярные вопросы