Найдите наибольшее и наименьшее значения функции
,
на отрезке

Область определения функции: x > 0

Рассмотрим два случая:

1) Если 0 < x < 1, то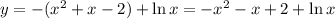

Получаем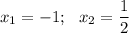 , но рассматриваемая точка экстремума положительная, поэтому откидываем значение x = -1.

(0)__+___(1/2)____-___(1)

Вертикальная асимптота: x = 0 и учитывая то, что функция возрастает с 0(не включая) до значения x=1/2, то у функции наименьшего значения нет.

2) Если 1 < x ≤ 2, то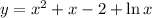 - возрастает на промежутке x > 1. Но на промежутке x ∈ (1; 2] будет наибольшее значение функции в точке x = 2 и равно оно 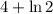. Наименьшего значения функции не существует.