Найдите наибольшее и наименьшее значение функции на отрезке: у = 2х^3 - 3х^2 - 12 [-2; 5]

Для начала найдем производную и приравняем ее к нулю:

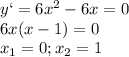
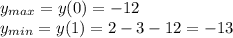
[-2]..+..{0}..-..{1}..+..[5]

Чтобы решать такие задачи, необходимо ученику знать, что такое производная. 

Алгоритм решения таков:

1)Подставляем конечные точки (в вашем случае - от -2 до 5) в функцию. Сравниваем результаты

2)Находим производную, приравниваем к 0 (т.е. находим экстремум функции)

Начнем с 1.

-16-12-12=-40

250-75-12=163

-40<163.

Находим экстремум:

6x²-6x

6x(x-1)=0

x₁=0;

x₂=1.

Вставляем найденные значения в функцию

0-0-12=-12

2-3-12=-13

Раз значений меньше нет, значит min=-40; max=163