Найдите наибольшее и наименьшее значение функции на отрезке f(x)=2x3+9x2+24x [-2;1]

Question

Алгебра: Найдите наибольшее и наименьшее значение функции на отрезке f(x)=2x3+9x2+24x [-2;1]

elenabeloglazo · Answer

Заметим, что функция монотонно возрастает на всей своей области определения (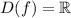 $D(f) = \mathbb R$ ).

Убедиться в этом можно и при производной:

$\Big (f(x) \Big )' = \Big (2x^3+9x^2+24x \Big ) ' = 6x^2 + 18x + 24$

Оказывается, что таких точек, где производная равна нолю, не существует (во всяком случае, в области действительных чисел):

$6x^2 + 18x + 24 = 0 \\x^2 + 3x + 4 = 0\\D = b^2 - 4ac = 3^2 - 4 \cdot 1 \cdot 4 = - 7$

Из этого следует, что максимальное значение функции на промежутке $[ \; -2; \; 1 \; ]$ достигается при x = 1 :

$f(1) = 2 \cdot 1^3 + 9 \cdot 1^2 + 24 \cdot 1 = 2 + 9 + 24 = 35$

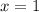А минимальное - при x = -2 :

$f(-2) = 2 \cdot (-2)^3 + 9 \cdot (-2)^2 + 24 \cdot (-2) = -16 + 36 - 48 = -28$

Задача решена!

ответ:

максимальное значение: 35 ;

минимальное значение: - 28 .