Найдите наи­мень­шее пя­ти­знач­ное число, крат­ное 55, про­из­ве­де­ние цифр ко­то­рого боль­ше 50, но мень­ше 75.

Число делится на 55 если оно делится и на 5 и на 11. По признаку делимости на 5, число делится на 5 тогда, когда его последняя цифра 0 или 5, но так как если последняя цифра будет 0, то произведение цифр пятизначных чисел будет 0, поэтому последняя цифра будет 5.

Для удобства назовем наше число abcde, где каждая буква обозначает конкретный разряд числа: a – десятки тысяч, b – тысячи, c – сотни, d – десятки и e – единицы.

Число делится на 11, если сумма цифр на нечётных местах равна сумме цифр на чётных местах:

По условию задачи: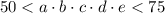 . Возможные значения произведения пятизначного числа : 55, 60, 65, 70 и разложим каждое число на простые множители

55 = 5 * 11

60 = 2 * 2 * 3 * 5

65 = 5 * 13

70 = 2 * 5 * 7

Перебираем возможные варианты составить числа и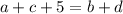

6, 5, 2, 1, 1 разбить никак

5, 4, 3, 1, 1: 5 + 1 + 1 = 4 + 3;   ⇒   14135, 13145

5, 3, 2, 2, 1 разбить никак

7, 5, 2, 1, 1: 5 + 2 + 1 = 7 + 1;    ⇒   27115, 21175, 17215, 11275

Отсюда наименьшее 11 275;  

ответ: 11 275.