Найдите множество значений функции g(x)=корень из x^2+4x+53
, )​

ответ: .

Для того чтобы найти множество значений функции g(x) = √(x^2 + 4x + 53), нужно сначала понять, какие значения может принимать выражение внутри корня.

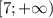Выражение x^2 + 4x + 53 является квадратным трехчленом и представляет собой параболу вида ax^2 + bx + c. Для определения множества значений этого выражения углубимся в анализ его дискриминанта (D).

D = b^2 - 4ac

В данном случае a = 1, b = 4 и c = 53. Подставим эти значения в формулу для D:

D = 4^2 - 4(1)(53)
D = 16 - 212
D = -196

Значение дискриминанта D равно -196. Если D отрицательное, это означает, что выражение x^2 + 4x + 53 не имеет действительных корней, а значит, не может стать отрицательным. Таким образом, для любых значений x выражение x^2 + 4x + 53 будет положительным.

Теперь, когда мы знаем, что выражение x^2 + 4x + 53 положительное для любых значений x, это означает, что можно извлечь из него квадратный корень. Извлекая корень из положительного числа, мы получаем положительный результат. Таким образом, множество значений функции g(x) представляет собой множество положительных чисел.

Ответ: Множество значений функции g(x) = √(x^2 + 4x + 53) - это множество положительных чисел.