Найдите косинус альфа, если синус альфа равен -2/3

cos^2a + sin^2a = 1

соответственно:

cos^2a = 1 - (-2/3)^2

cos^2a =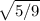

cos a = +-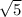  / 3

Объяснение:

Объяснение:

По основному тригонометрическому тождеству

sin^2 a + cos^2 a = 1

cos^2 a = 1 - sin^2 a = 1 - (-2/3)^2 = 1 - 4/9 = 5/9

cos a1 = √(5/9) = √5/3, если угол лежит в 4 четверти, 3Π/2 < a < 2Π

cos a2 = -√(5/9) = -√5/3, если угол лежит в 3 четверти, Π < a < 3Π/2

Объяснение:

Если известно sinα, то cosα легко находим с основного тригонометрического тождества

sin²α + cos²α ≡ 1.

Отсюда, так как sinα = -2/3, то

cos²α = 1 - sin²α = 1 - (-2/3)² = 1 - 4/9 = 5/9.

Тогда

Далее, sinα<0, то π < α < 2·π. Тогда, если

π < α < 3·π/2, где косинус отрицательный, то

3·π/2 < α < 2·π, где косинус положительный, то