Найдите корни уравнения 4х^2+7х-11=0​

Объяснение:

Я действовал путем разложения на множители путем группировки.

1. Чтобы решить уравнение, нужно разложить левую сторону на множители путем группировки. Сначала левую сторону необходимо перезаписать в следующем виде: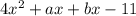 . Чтобы найти a и b, нужно настроить систему для решения.

2. Так как ab отрицательный, a и b имеют противоположные знаки. Поскольку результат выражения a+b положительный, положительное число имеет больше абсолютное значение, чем отрицательное. Тогда, нужно перечислить все такие пары, содержащие −44 продукта.

3. Потом вычислить сумму для каждой пары.

4. Решение это пара значений, сумма которых равна 7.

5. Затем надо переписать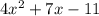 как :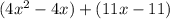

6. Вынести за скобки 4x в первой и 11 во второй группе.

7. Потом вынести за скобки общий член x−1, используя свойство дистрибутивности.

8. Чтобы найти решения для уравнений, надо решить x−1=0 и 4x+11=0.

4х²+7х-11=0​

х=(-7±√(49+176))/8=(-7±5)/8, но короче по Виету. Сумма корней   -7/4, произведение -11/4, это числа  1 и -11/4