1. Алгебра
  2. Найдите корни уравнений cos(x/2)+sin(x/2)=1.

Найдите корни уравнений cos(x/2)+sin(x/2)=1. (-180°; 180°)

Ali20091 Ali20091    1   29.05.2019 13:08    2

Ответы
Жизель24 Жизель24  28.06.2020 16:22

x\in (-\pi;\pi)\Rightarrow t= \frac{x}{2}\in (-\frac{\pi}{2};\frac{\pi}{2}).

Если t лежит в 4-й четверти, синус отрицателен, поэтому сумма синуса и косинуса не может равняться 1 (ведь оба они лежат в пределах между минус 1 и 1). Поэтому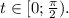 t\in [0;\frac{\pi}{2}).  Если t=0, то cos t=1, sin t=0, то есть t=0 является решением. Если

t=\in (0;\frac{\pi}{2})\Rightarrow \left \{ {{0<\cos t<1} \atop {0<\sin t<1}} \right. \Rightarrow \left \{ {{\cos t\cos^2 t} \atop {\sin t\sin^2 t}} \right.\Rightarrow \cos t+\sin t\cos^2 t+\sin^2 t=1,

то есть на этом промежутке решений нет. Поэтому единственное решение t=0, откуда x=0.

ответ: 0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Aydan204 Aydan204  08.09.2019 21:50
Нужно доказательство попроще теорема: из точки не лежащей на прямой можно провести перпендикуляр к этой прямой и при том только 1....
Rtyrtya Rtyrtya  08.09.2019 21:50
1) 6√х=46 2) 3х^2-300х=0 3) 25х^2=81...
atom33 atom33  08.09.2019 21:50
Log 1/3 x+log 1/3 y=2 log 1/3 x-log 1/3 y=4 это система. решить...
zero161 zero161  28.05.2019 01:10
Преобразуйте уравнение в квадратное и назовите его коэффициенты! решите уравнение: найдите корни уравнения:...
kirilsex69 kirilsex69  28.05.2019 01:10
Не выполняя построений, найдите координаты точки пересечения графиков уравнений: решить уравнение a) 7x+4y=23 и 8x-10y=19...
лим0н лим0н  28.05.2019 01:10
Постройте график функции y= -1,5sin(x-2π/3) +2...
ksuholina ksuholina  28.05.2019 01:10
Многочлен к стандартному виду и найдите его значение при а = 1 , b = -1 : 3b^2 + a^2 * b + 5ab^2 + 4a^2 * b - 5ab^2 - 3b^2 !...
DanilkaMare DanilkaMare  28.05.2019 01:10
Решите систему уравнений методом подстановки 4x+y=49 -x+y=17...
Lunitoes Lunitoes  18.11.2020 12:37
до 18:00 контроша алгебра ​...
alis2710p00nvt alis2710p00nvt  18.11.2020 12:37
Fx=x3-ax2+7x+5     gx=2x2-5x+2 Найти наклон касательной в точке x = 2​...

Популярные вопросы