Найдите координаты точки пересечения графиков функций у = 2 −
2
3
х и
у = 3х – 9.
Другие вопросы по теме Алгебра
Популярные вопросы
- Велосипедист проехал со скоростью 15 км в час, всадник 12 км/ч, время одинаковое...
3 - Как называются области земли , в которых происходит 95 % землетрясений....
1 - Заполните таблицу бактерии 1.польза 2.вред...
3 - Как называется машина которая сажает картофель?...
3 - Замените имена прилагательные в данных словосочетания антонимам.несчастный...
3 - Сколько 27гектаров в 1)квадратных метрах 2)в квадратных километрах...
3 - Какие склоняемые,а какие несклоняемые имена сущ. серебро,поле,кофе,пальто,яблоко,небо,самбо,дерево,чувство,какао,драже,турне,море,фойе...
2 - Фонетический разбор слова зарубежных...
2 - Что означает фразеологизм заговаривать зубы водить вокруг пальца пальчики...
3 - Выручайте, объясните как определить азимут без компаса с транспортиром,...
1
y = 2 - 23x y = 3x - 9
2 - 23x = 3x - 9
- 23x - 3x = - 9 - 2
- 26x = - 11
Приравниваем и решаем как уравнение:
Подставляем значение аргумента:
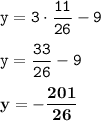
ответ: