Найдите какую-нибудь пару натуральных чисел, которая являет- ся решением уравнения
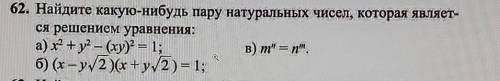
Другие вопросы по теме Алгебра
Популярные вопросы
- Гімн України 1 Розкажи про засоби музичної виразності головної пісні...
1 - Как найти радиус описанной окружности?...
1 - Қоңыр салқын,дөнделі морфологиялық талдау жасау ...
2 - Какое минимальное число спороцитов страусника необходимо, чтобы на...
3 - К какой культуре относится африка?...
1 - Корневые волоски представляют собой Укажите правильный вариант ответа:...
2 - Карошо к кому из героев Сочувствую Почему...
1 - Проект «ДОБРО НАЧИНАЕТСЯ С МЕНЯ»•Чему я учусь у своих родителей?•Нравится...
1 - 2). Визначте рядок, у якому в реченні прикладка з означуваним словом...
3 - Ребят сделаю все что захотите,переведу 50 рублей если решите.1)в...
3
Найти по одному решению каждого уравнения - не проблема. А вот найти все натуральные решения - это намного более сложная задача.
Простейшие решения в первой задаче (1;1)), во второй (3;2), в третьей (1;1). Дальше можете не смотреть (а можете посмотреть).
1) Преобразуем так: (x²-1)(y²-1)=0; x²-1=0 или y²-1=0; x=1 или y=1.
То есть решения такие: (1;1), (1;2), (1;3), ..., (2;1), (3;1),...
2) Преобразуем так: x²-2y²=1. Это намного более сложная задача - частный случай так называемого уравнения Пелля. Заинтересуетесь - почитайте литературу на эту тему, только сначала попробуйте решить сами. Годится, как я уже писал, пара (3;2), остальные пары получаются из этой по такому правилу: если была пара (x;y), то следующая равна (3x+4y;2x+3y). Поэтому получаем второе решение (3·3+4·2;2·3+3·2)=(17;12). Можете построить сколько угодно решений по такому правилу.
3) Конечно, если m=n, то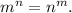 Поэтому мы уже имеем бесконечное множество решений. Но ими множество решений не исчерпывается. По крайней мере
Поэтому мы уже имеем бесконечное множество решений. Но ими множество решений не исчерпывается. По крайней мере 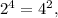 то есть получили решения (2;4) и (4;2). Докажем, что других решений нет. Преобразуем так:
то есть получили решения (2;4) и (4;2). Докажем, что других решений нет. Преобразуем так: ![\sqrt[m]{m}=\sqrt[n]{n}.](/tpl/images/4529/0693/329fd.png)
Рассмотрим функцию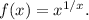 (x≥1)
(x≥1)
Слева от e производная положительна, справа отрицательна, то есть слева от e функция возрастает, справа убывает.
ответ в третьей задаче: (2;4), (4;2), (1;1), (2;2), (3;3),...
прощения, если не все было понятно - в будущем разберетесь))