Найдите график функции
1) y=3 дробь (х+5) +2
2)у=-1 дробь (х-3) +4
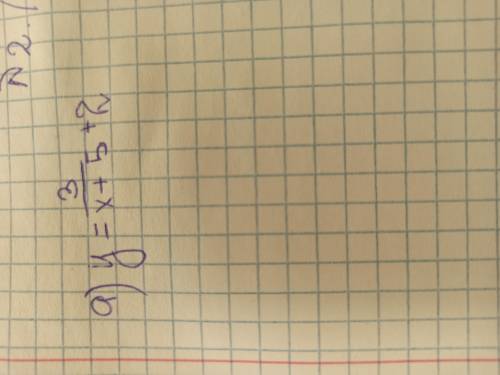
Другие вопросы по теме Алгебра
Популярные вопросы
- Известно, что сумма числителя и знаменателя дроби равна 52 (числитель...
1 - Решить по 8 класс выполните превращения по следующим схемам:...
2 - Вподчеркнутом предложение найди и подчеркни основу предложение-...
2 - На шахматную доску надо поставить короля и ферзя. сколькими это...
2 - 1.сравните 0,675 и 16/25; 0,84 и 13/15 2.докажите неравенство...
3 - Выполни действия 1) 17/54 * 15/34 2) 1 целая 1/15 : 4 целые 3/5...
1 - Выпишите из текста словосочетания,в которых главным словом является...
1 - Yesterday my friend and the history museum. old clothes and old...
1 - Заранее ) обсуждены. морфологический разбор...
3 - ☺надо придумать вопросы к рассказу петька на даче...
1
Шаг 1: Начнем с первой функции y=3/(x+5)+2.
Для построения графика функции, мы будем использовать таблицу значений. Выберем несколько значений для переменной x и найдем соответствующие значения для переменной y.
Выберем значения для x: -5, -4, -3, -2, -1, 0, 1, 2 и 3.
Подставим эти значения в функцию и найдем значения для y:
Когда x=-5:
y = 3/(-5+5)+2
y = 3/0+2
Это значение неопределено, так как не можем делить на ноль. Запишем его как (x, y), где x=-5, y = неопределено.
Когда x=-4:
y = 3/(-4+5)+2
y = 3/1+2
y = 3+2
y = 5
Записываем (x, y) = (-4, 5).
Когда x=-3:
y = 3/(-3+5)+2
y = 3/2+2
y = 3/2+4/2
y = 7/2
Записываем (x, y) = (-3, 7/2).
Когда x=-2:
y = 3/(-2+5)+2
y = 3/3+2
y = 1+2
y = 3
Записываем (x, y) = (-2, 3).
Когда x=-1:
y = 3/(-1+5)+2
y = 3/4+2
y = 3/4+8/4
y = 11/4
Записываем (x, y) = (-1, 11/4).
Когда x=0:
y = 3/(0+5)+2
y = 3/5+2
y = 3/5+10/5
y = 13/5
Записываем (x, y) = (0, 13/5).
Когда x=1:
y = 3/(1+5)+2
y = 3/6+2
y = 3/6+12/6
y = 15/6
Записываем (x, y) = (1, 15/6).
Когда x=2:
y = 3/(2+5)+2
y = 3/7+2
y = 3/7+14/7
y = 17/7
Записываем (x, y) = (2, 17/7).
Когда x=3:
y = 3/(3+5)+2
y = 3/8+2
y = 3/8+16/8
y = 19/8
Записываем (x, y) = (3, 19/8).
Теперь у нас есть несколько значений для построения графика функции y=3/(x+5)+2: (-5, неопределено), (-4, 5), (-3, 7/2), (-2, 3), (-1, 11/4), (0, 13/5), (1, 15/6), (2, 17/7) и (3, 19/8).
Шаг 2: Построим график функции y=3/(x+5)+2 на координатной плоскости.
Выберем масштаб, чтобы уместить все точки. Для удобства, можно взять интервалы по x и y следующие: x от -6 до 4 и y от -1 до 6.
Нанесем на координатную плоскость все точки, которые мы нашли для построения графика.
Теперь соединим все эти точки гладкой кривой. Обратите внимание, что график будет проходить через точки (-4, 5), (-3, 7/2), (-2, 3), (-1, 11/4), (0, 13/5), (1, 15/6), (2, 17/7) и (3, 19/8), а неопределенная точка (-5, неопределено) показывает график, в котором функция становится бесконечно большой когда x приближается к -5.
Это и есть график функции y=3/(x+5)+2.
Теперь перейдем ко второй функции y=-1/(x-3)+4.
Также построим таблицу значений и выберем несколько значений для переменной x: -2, -1, 0, 1, 2, 3, 4, 5 и 6.
Подставляем эти значения в функцию и находим значения для y:
Когда x=-2:
y = -1/(-2-3)+4
y = -1/-5+4
y = 1/5+20/5
y = 21/5
Записываем (x, y) = (-2, 21/5).
Когда x=-1:
y = -1/(-1-3)+4
y = -1/-4+4
y = 1/4+16/4
y = 17/4
Записываем (x, y) = (-1, 17/4).
Когда x=0:
y = -1/(0-3)+4
y = -1/-3+4
y = 1/3+12/3
y = 13/3
Записываем (x, y) = (0, 13/3).
Когда x=1:
y = -1/(1-3)+4
y = -1/-2+4
y = 1/2+8/2
y = 9/2
Записываем (x, y) = (1, 9/2).
Когда x=2:
y = -1/(2-3)+4
y = -1/-1+4
y = 1+4
y = 5
Записываем (x, y) = (2, 5).
Когда x=3:
y = -1/(3-3)+4
y = -1/0+4
Это значение неопределено, так как не можем делить на ноль. Запишем его как (x, y), где x=3, y = неопределено.
Когда x=4:
y = -1/(4-3)+4
y = -1/1+4
y = -1+4
y = 3
Записываем (x, y) = (4, 3).
Когда x=5:
y = -1/(5-3)+4
y = -1/2+4
y = -1/2+8/2
y = 7/2
Записываем (x, y) = (5, 7/2).
Когда x=6:
y = -1/(6-3)+4
y = -1/3+4
y = -1/3+12/3
y = 11/3
Записываем (x, y) = (6, 11/3).
Теперь, используя полученные значения, построим график функции y=-1/(x-3)+4.
Выберем тот же масштаб для осей, что и раньше, и нанесем все точки на координатную плоскость.
Теперь соединим все эти точки гладкой кривой. График будет проходить через точки (-2, 21/5), (-1, 17/4), (0, 13/3), (1, 9/2), (2, 5), (4, 3), (5, 7/2) и (6, 11/3), а точка (3, неопределено) показывает, что график становится бесконечно большим, когда x приближается к 3.
И вот, график функции y=-1/(x-3)+4 готов.
Надеюсь, эти подробные пояснения помогут вам лучше понять, как построить график данных функций.
[Примечание: По предоставленному изображению график не может быть воссоздан с точностью, поэтому вам нужно провести линии через точки, чтобы получить примерный вид графика функции. Идеальное решение можно получить только с помощью математического анализа.]