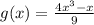 Найдите g(−2)+g(2). Обьясните решение !
Найдите g(−2)+g(2). Обьясните решение !
Другие вопросы по теме Алгебра
Популярные вопросы
- Жил в деревне- приехал в деревню. вышел на берег- отдыхал на берегу. удалился...
3 - Решить 32_05*(28_03+11,5)-1266,9365...
2 - Как правильно пишется слово грустчу гостщу...
3 - Умальчика в коллекции было 24 болгарские марки и 40 российских марок. он поместил...
3 - Как найти площадь треугольника со сторонами 9см, 8см, 4см?...
1 - Тело весит в воздухе 6н, а в воде 4н. найти плотность этого тела....
2 - Progress check test 9 (the past simple/the past continuous) choose the appropriate...
3 - Образуй от глагола играть по одному глаголу в формах настоящего будущего времени....
1 - Подберите прилагательные с противоположным значением. пустых,долгую,свежее,нетолстый....
3 - Вслове бочка есть мягкий согласный звук...
3
Самое понятное, что можно сделать - просто подставить и посчитать:
Можно было заметить, что заданная функция нечетная:
Тогда, на основе этого получим:
ответ: 0