Найдите действительные решения системы уравнений
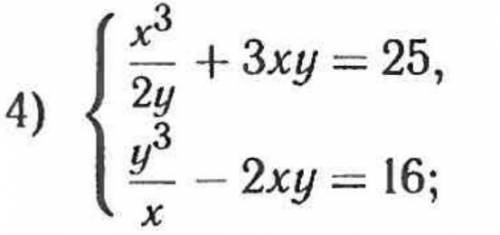
Другие вопросы по теме Алгебра
Популярные вопросы
- Как получить газообразное вещество ?...
2 - Рост стебля дерева в толщину происходят за счет а) луба,б)камбия,в)ксилемы,г)флоэмы...
3 - Какой город— камберра или кейптаун — расположен южнее?...
1 - Закончить предложение расположение гор и равнин связано со...
2 - Как из ca(hco3)2 получить caso4 * 2h2o и из caso4 * 2h2o получить (caso4)2...
3 - Сбольшим усердеем бах изучал музыку провославленных ,и композиторов,таких...
2 - 1. необходимым для всех реакций веществом в клетке, играющим роль растворителя...
1 - Напишите мне сочинение о романе дубровском зарание...
3 - Существует мнение что погода влияет на самочувствие человека и я в этом не...
2 - Правила поведения современного рыцаря...
1
ответ: (2;4);(-2;-4)
Объяснение:
ОДЗ: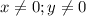
Вычитаем второе уравнение из первого:
Учитывая, что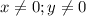 , можно поделить обе части уравнения на
, можно поделить обе части уравнения на 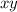 :
:
Тут решений нет.