1. Алгебра
  2. Найдите cos l, если sosl= (корень91)/10

Найдите cos l, если sosl= (корень91)/10 и l (0.5п; п)

даша3646 даша3646    2   10.03.2019 06:20    0

Ответы
Partners04 Partners04  24.05.2020 14:16

sinL=\frac{\sqrt{91}}{10}

cos^2L=1-sin^2L

cos^2L=1-(\frac{\sqrt{91}}{10})^2=1-\frac{91}{100}=\frac{100-91}{100}=\frac{9}{100}

cosL=\sqrt{cos^2L}=\sqrt{\frac{9}{100}}=\frac{3}{10}

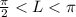Т.к. \frac{\pi}{2}< L <\pi, а знак косинуса во 2-й четверти отрицателен: значит ответ: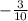 -\frac{3}{10}

ПОКАЗАТЬ ОТВЕТЫ
muy5 muy5  24.05.2020 14:16

из формулы sin^2L+cos^2L=1, найдем cosL=корень(1-sin^2L), так как по условии L в 2 четверти, то cosL=-sqrt(1-sin^2L)=-sqrt(1-91/100)=-sqrt(9/100)=-3/10=-0,3.

ответ: -0,3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kirillavinov kirillavinov  14.09.2020 15:33
7.Спростіть вираз -4(6-2а)-2(a-8) І знайдіть його значення, якщо а-0,1​...
Nikyyysik Nikyyysik  14.09.2020 15:33
1.97 замените дробью степень с целым отрицательным показательным 1)3^-3 2)2^-3 3)5^-2 4)a^-2 5)b^-10 6)x^-7...
Голес Голес  14.09.2020 15:31
В упражнениях 1.23-1.38 решите системы уравнений....
kistina2 kistina2  14.09.2020 15:31
А) 36 57. Какие из следующих выражений имеют смысл:г) (-7); ж) yь - 1, где b = 1;б) -4;д) -93) у 3-с, где с 3?в) - 0,01; е) -а, где a 0:помагите...
sasha228h sasha228h  14.09.2020 15:30
Найдите значение дроби, предварительно сократив ее.​...
zizigi zizigi  14.09.2020 15:29
6.При яких значеннях в рівняння 3х= 8х + 12 =0 має один корінь? (2 6)​...
дана399 дана399  14.09.2020 15:29
плз. 0,3 х * (-12у) = -3,6ху. -6,2а*5 = - 31а...
BlankDawn BlankDawn  14.09.2020 15:29
Складіть квадратне рівняння із цілими коефіцієнтами корені якого дорівнюють 1/8 і 1/2​...
kocrtaru kocrtaru  14.09.2020 15:29
Доходность инвестиций 12% инфляция8%...
pornuxa1 pornuxa1  14.09.2020 15:29
№1. Постройте график функции f(x), где f(x) = (x?, если -3 x 0-Зх, если 0 x 3С графика найти:а) f(-1); f(1); f(2); f(-2); f(-3); f(3);б) значение х, при которых f(x)=0;f(x)=4;...

Популярные вопросы