Найдите cos α, если 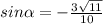 и ∈ (1,5
и ∈ (1,5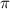 ; 2
; 2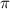 )
)
Другие вопросы по теме Алгебра
Популярные вопросы
- Яка маса оцетової кислоти 10% необхідно для нельтралізації розчину лугу масою...
3 - 3 1 Complete the sentences with the passiveform of the verb in brackets and...
3 - 9х — 8 |у - 5| при х = -8, у = -8....
1 - Как переводится на казахский празнуем...
1 - Три плюс три-шість. У реченні числівник шість виконує роль....
1 - Дано точки О і А . Побудуйте точку А , в яку переходить точка А при повороті...
1 - Составить словосочетания с переходными глаголами(10 предложений, 2 с Р. п,2...
3 - Аварийный участок тротуара прямоугольной формы загородили красной лентой....
2 - Сделайте блок схему с Линейной сортировкой...
1 - Из пункта А в пункт В расстояние между которыми 27 км вышел турист. через...
2
Так как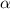 ∈ 1,5π;2π , то
∈ 1,5π;2π , то 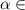 4 четверти, косинус 4й четверти +
4 четверти, косинус 4й четверти +
Из основного тригонометрического тождества sin²∝ + cos²∝ = 1 выразим cos∝
cos∝= √1-sin²∝
Т.к. ∝∈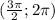 ⇒ cos∝ будет положительным
⇒ cos∝ будет положительным
ответ: cos∝= 0,1