Найдите cos(60°+α), если sin α=0,6 и 0 < α < π/2
Другие вопросы по теме Алгебра
Популярные вопросы
- Where is bill? where are kate and tom? where are nick and vicky? where are...
3 - Составить словосочетания со словами: поразительный, дивный, чудесный...
2 - 2agno3+h2so4=2hno3+ag2so4 написать полное и сокращённое ионное соединения...
2 - Какая масса осадка образуется при взаимодействии 20г. ba(oh)2 с серной кислотой...
2 - Тело под действием силы 10н передвигается в направлении действия силы на расстояние...
3 - От названия какой игры в языке образован глагол со значением-отослать,отправить...
1 - Запиши вопросы. 1) there is a small field next to the house is there 2)people...
3 - 1.столица халифата при аббасидах. 2.столица арабского халифата в vii-первой...
1 - Напишите два примера разных молекулярных уравнений,которые соответствуют сокращённому...
2 - Воду из мензурки перелили в сосуд, нагреваемый паяльной лампой, до 100 градусов....
2
Так как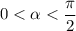 , то это угол первой четверти, где все тригонометрический функции положительны.
, то это угол первой четверти, где все тригонометрический функции положительны.
Искомое выражение: