найдите число целочисленных решений неравенства
нужно заранье

По тереме Виета корнями уравнения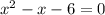   будут числа  -2 и 3, значит:

Так как 2>0 и 3>0, то система неравенств упрощается:

1)

          +                         -                                +

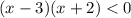
__________-2___________3__________________

Решение первого неравенства:  -2 < x < 3

2)

     это решение второго неравенства

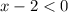
3) Общее решение: -2 < x < 2

Перечислим целочисленные решения из этого промежутка:

-1;  0;  1

Всего три!

ответ: 3