1. Алгебра
  2. Найдите целое значение параметра

Найдите целое значение параметра a, при котором сумма квадратов корней уравнения
x^{2} +x-2\alpha x+4+a^{2}

принимает наименьшее значение.

toshakotik toshakotik    2   12.10.2019 14:44    1

Ответы
ПандаВера ПандаВера  06.08.2020 10:22

x^2+x-2ax+4+a^2=0\\ x^2-(2a-1)x+a^2+4=0

По теореме Виета:

x_1+x_2=2a-1\\ x_1x_2=a^2+4

Сумма квадратов корней :

x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(2a-1)^2-2\cdot (a^2+4)=\\ \\ =4a^2-4a+4-2a^2-8=2a^2-4a-4

Сумма квадратов принимает наименьшее значение, если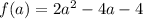 f(a)=2a^2-4a-4 достигает наименьшего значения, а поскольку графиком функции является парабола, с ветвями направленными вверх, то вершина параболы достигает минимума.

a=-\dfrac{-4}{2\cdot 2}=1

ответ: a = 1.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
k666goblin k666goblin  07.06.2019 03:40
Докажите тождества tgx+ctgx=2/sin2x...
579w2g3 579w2g3  07.06.2019 03:40
Докажите тождества tgx+ctgx=2/sin2x...
1o10019soos 1o10019soos  07.06.2019 03:40
Я решите мне это уравнение.. tg2x=3sinx...
Pollyyyyyyyyyyyyyyy Pollyyyyyyyyyyyyyyy  07.06.2019 03:40
Системы уравнений 2х-3у=1 х+у=6 х+у=7 3х+у=2 3х-2у=9 5-7у=11 ! буду : ***); ))***...
Валерушка8 Валерушка8  07.06.2019 03:40
Вдетский сад 27 литров яблочного и томатного сока в трехлитровых банках.томатного 5 банок.сколько банок яблочного сока ?...
lebedeva2303 lebedeva2303  07.06.2019 03:40
Разложите на множители: 2(m+n)+km+km...
Pmoshnek Pmoshnek  07.06.2019 03:40
№2 выражение и найдите его значение: а) (а-7)в квадрате 2+(а+14)при а=0,5 б)9m(m--1)в квадрате, при m= -- дробь(1/3)...
Baka1111 Baka1111  07.06.2019 03:40
Найдите значение выражения ,вот этот знак ^ означает степень! 36 умножить на(1/3)^3+6 умножить на(1/3)^2...
Vergoon Vergoon  11.07.2019 07:10
Кбассейну объёмом 1200м3 подведены 2 трубы: и отводящая. если открыть одновременно обе трубы то бассейн заполнится за 60 часов. если же открыта только одна труба, то заполнение...
Wasder1 Wasder1  11.07.2019 07:10
Решите неравенство: 5(4y+ 7)- 38 11- 6(3y- 4)...

Популярные вопросы