1. Алгебра
  2. Найди сумму всех натуральных

Найди сумму всех натуральных чисел ,не превосходящих 170,которые при делении на 4 дают остаток 1

bandit12341 bandit12341    3   15.03.2020 21:13    9

Ответы
Nikki21 Nikki21  23.08.2020 16:10

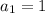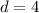Это арифметическая прогрессия с a_1=1 и d=4. Составим формулу n-ого члена:

a_n=a_1+d(n-1)

a_n=1+4(n-1)

Определим число n:

1+4(n-1)\leq 170

4(n-1)\leq 169

n-1\leq \dfrac{169}{4}

n\leq \dfrac{173}{4}

n\leq 43\dfrac{1}{4}

Учитывая, что n - натуральное, номер последнего интересующего нас члена арифметической прогрессии равен 43.

Находим сумму:

S_{n}=\dfrac{2a_1+d(n-1)}{2}\cdot n

S_{43}=\dfrac{2\cdot1+4\cdot42}{2}\cdot 43=3655

ответ: 3655

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Маруська246 Маруська246  17.05.2019 18:40
Решить квадратные уравнения с дискриминант 1)3x^2+7x+2=0 2)2x^2+x+1=0 3)4x^2+4x+1=0 4)x^2-2x+2=0 5)5x^2-3x+8=0...
Igor599 Igor599  17.05.2019 18:40
Дана гкометрическая пргрессия bn,вычислить сумму двух первых членов,если bn: -24 q: - 2...
kotBarsik14 kotBarsik14  17.05.2019 18:50
Между числами 2 и -18 корень 3, вставьте 4 числа так чтобы получилась прогрессия....
Alex71532 Alex71532  17.05.2019 18:50
Решите : в зрительном зале клуба 320 мест. после того как число мест в каждом ряду увеличили на 4 и добавили один ряд, в зале стало 420.сколько рядов стало в зрительном зале клуба?...
lerkakotik1983 lerkakotik1983  17.05.2019 18:50
1)y=9/x+3 и y=x-5 2)y=4/x-1 и y=x-4 если можно пишите решение...
danya13112004 danya13112004  17.05.2019 18:50
Магазин продаёт ткань четырёх видов - ситец , шерсть , вельвет и полотно . за день было продано 124,8 м ситца , шерсти - в 10 раз меньше , чем ситца , вельвета - на 49,9м больше ,...
VasyPupok228 VasyPupok228  17.05.2019 18:50
Когда самолёт находится в горизонтальном полёте ,подъёмная сила,действующая на крылья,зависит только от скорости .определите по рисунку ,на сколько увеличиться подъемная сила ( в...
coopersmith coopersmith  17.05.2019 18:50
Необходимо найти корни уравнения 2sin x + sin 2x =cos x + 1 на интервале [0; п]...
ПростоМиха ПростоМиха  17.05.2019 18:50
Какие из чисел корень квадратный из 18, корень квадратный из 26, корень квадратный из 30 заключены между числами 5 и 6?...
wwwzelenruowzl2z wwwzelenruowzl2z  17.05.2019 18:50
Расположите на простые множители числа 156 208...

Популярные вопросы