Найди промежутки убывания функции y=2x−4. Выбери правильный вариант ответа.
Функция y=2x−4 убывает при
x∈(−∞;−1,9)∪(−1,9;+∞)
x∈(−∞;+∞)
x∈(−∞;4)∪(4;+∞)
x∈(−∞;−4]
x∈(−∞;−1,9]
x∈(−∞;0)∪(0;+∞)
x∈[−4;+∞)
x∈[1,9;+∞)
Другие вопросы по теме Алгебра
Популярные вопросы
- (до 18:00 сдать нужно, сейчас у меня без 10 3.) Фото: >...
1 - Дети играют в прятки. Серёжа – водящий. Он стоит лицом к дереву,...
2 - Підсумкова контрольна робота за 2019 – 2020 н.р. Термін виконання:...
3 - Учні класу зібрались на екскурсію. Якщо кожен учень здасть на екскурсію...
1 - написать уравнение касательной к графику функции уравнение на фото...
3 - Ребята Надо поставить предложиения в правильном порядке. 1.За столом...
1 - Установіть пропущені назви земель України...
2 - ПИСЬМЕННО ПИШИТЕ!) ЗАРАНЕЕ Дайте определение смеси. Что означает...
1 - плачу До розчину літій карбонату масою 200 г із масовою часткою...
3 - Два угла, вписанного в окружность четырехугольника равны 64 ° и...
1
Функция не имеет промежутков убывания
Объяснение:
По теореме если угловой коэффициент прямой меньше нуля, то функция убывает, а если угловой коэффициент прямой больше нуля, то функция возрастает.
Докажем теорему
Рассмотрим функцию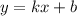 .Где x,y - переменные; k,b - параметры. Продифференцируем функцию y.
.Где x,y - переменные; k,b - параметры. Продифференцируем функцию y.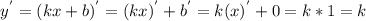
По теореме если производная больше нуля на промежутке M, то на этом промежутке функция возрастает.
По теореме если производная меньше нуля на промежутке M, то на этом промежутке функция убывает.
Тогда согласно теоремам:
если k < 0, то функция убывает.
если k > 0, то функция возрастает.
y=2x − 4 ⇒ k > 0, тогда функция возрастает при x є R.