Найди производную функции:у(х)= 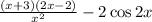
Другие вопросы по теме Алгебра
Популярные вопросы
- решить задачу Из двух городов Одновременно навстречу друг другу выехали грузовик...
3 - Объясните почему в хим. формулах число валентности одного элемента должно быть...
2 - буду безмерно благодарна (максимально подробно...
2 - Выпишите из текста сначала двусоставные предложения и укажите главные члены,...
3 - Культурные растения и их полезные свойства технология 5 класс...
3 - Раскройте скобки в приводимых ниже предложениях, употребив личные местоимения...
3 - Задание 1 (письменно) Объяснить написание не с различными частями речи: Не(у)кого...
3 - Установіть ризики, що загрожують вам в інформаційному суспільстві...
1 - Сколько раз будет выполнен этот цикл? i = 4 while i 2: print ( Привет! ) i +=...
1 - Определите лицо, число, спряжение глаголов-журчат, появляется, лежит, строят,...
2
Объяснение:
Пусть:
а)
б)
в)
1)
2)