1. Алгебра
  2. (( найди область определения

((
найди область определения и область значения функции y=x2/x2+1

sharudakatya25oxzgq7 sharudakatya25oxzgq7    1   26.07.2022 11:46    1

Ответы
elizaveta1705fomina elizaveta1705fomina  26.07.2022 11:47

ответ.

 Область определения функции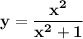  \bf y=\dfrac{x^2}{x^2+1}   - множество всех

действительных чисел ,  x\in D(y)\ ,  \boldsymbol{D(y)=(-\infty ;+\infty )}  , так как знаменатель дроби не обращается в 0 ни при каких значениях переменной  х . 

Заданная функция принимает только неотрицательные значения, так как эта функция в числителе имеет выражение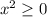  x^2\geq 0 , а в знаменателе  x^2+1\geq 1  .

Минимальное значение, которое принимает функция, равно 0 при х=0 .

Максимальное значение  стремится к 1 , так как  

\dfrac{x^2}{x^2+1}=\dfrac{x^2+1-1}{x^2+1}=1-\dfrac{1}{x^2+1}  .  

От 1 отнимается очень маленькое положительное значение , причём, чем больше значение  х  , тем меньшая величина вычитается . Значения, равное 1 , функция никогда не достигнет, но стремится к этому . Прямая у=1 является горизонтальной асимптотой графика . График показан на рисунке .

Поэтому область значений функции -  y\in E(y)\ \ ,\ \ \bf E(y)=[\ 0\ ;\ 1\ )   .                      


(( найди область определения и область значения функции y=x2/x2+1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
mrudaa717 mrudaa717  20.03.2019 08:03
Построить график функции у=1/3х-4 с построенного графика найти: 1. значение х, при котором значение функции равно -3 2. значение функции при х равном 3 3. два значения х,...
andrievskiyvitaliy andrievskiyvitaliy  20.03.2019 08:50
При каком значении х значений выражений х в квадрате -6х-1и 6+х в квадрате +х равны...
555Sofiya5555 555Sofiya5555  20.03.2019 08:50
Xквадрат -10xy+ 25 y квадрат решить...
ramon8 ramon8  20.03.2019 08:00
1) f(x) =x^4(5+2x-x^2) 2) f(x) =корень 8-x^3 3) y=cos x + tg x 4) f(x)=12x+3x^2-2x^3 5) f(x)=x^4-2x^2+4 (найти наименьшее значение, это к 5) [-1/2; 1/2] 6) f(x)=3^x/2^x+5^x...
ivansivalov ivansivalov  20.03.2019 07:59
Как можно быстрее, . 2. придумайте 2 показательных уравнения, равносильных уравнению: (2 целых 1/3)^x+7 = 9/49 3. log (x^2-6x) по основанию 0,99 log (6x-35) по основанию...
omarckina2010 omarckina2010  20.03.2019 07:58
Найти к , если известно, что график функции у=кх-6 проходит через точку р(-2; 8)...
iliasbro87073799809 iliasbro87073799809  20.03.2019 08:50
Вчемпионате по гимнастике участвуют 65 спортсменок . 17 из испании 22 из португалии остальные из италии . порядок в котором выступают гимнастки определяется жребием . найдите...
gladishsofiya gladishsofiya  20.03.2019 07:57
Преобразуйте в многочлен (у-9)²-3y(y+1)​...
iraapukhtina7 iraapukhtina7  20.03.2019 07:53
Построить график функции у=-3+5 с построенного графика найти: 1. значение х, при котором значение функции равно 8 2. значение функции при х , равном -1 3. два значения х,...
anitamirzikkk anitamirzikkk  20.03.2019 07:51
Преобразуйте в многочлен 3(x-4)²-3x² ​...

Популярные вопросы