Найди наибольшее и наименьшее значения функции x(t)=2t^5−2t+7, если 1≤t≤2.
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить про скорость для 5 класса...
3 - 1.перимет параллелограмма равен 16см. чему равен стороны параллеограмма,...
1 - Даны точки а(2; 2) b(6; -5) c(4; -4) найдите длину медианы вм треугольника...
2 - Из чердачного окошка выходят собака и кошка. вдвоем веселее дорожка залезшим...
1 - Ушынар в копилке 80 монет достоинством 20 тенге и 50 тенге. всего 2590...
1 - Угадайте корень уравнения: 3*х-х*х=0...
1 - Дно мирового океана исследовал: 1. тур хейурдал 2.жак пикар 3.норгей тенсинг...
1 - Выпеши слова которые состоят из одного слога двух слогов трех слогов раздели...
1 - Найди и выпиши слова которые отвечают на вопросы какой? какая? какое? какие?...
2 - Кто может как сказать это по tom: what s this? sam: it s a photo of my...
2
↓↓↓↓↓↓ ↓↓↓↓↓↓↓↓ ↓↓↓↓↓↓
Объяснение:
x(t)=2t⁵−2t+7,
x' (t)=10t⁴−2=2(5t⁴-1) , 5t⁴-1=0 , t⁴=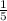 , t=±
, t=± ![\frac{1}{\sqrt[4]{5} }](/tpl/images/1364/7503/107ce.png)
x' (t)=0 при . t=±![\frac{1}{\sqrt[4]{5} }](/tpl/images/1364/7503/107ce.png)
±![\frac{1}{\sqrt[4]{5} }](/tpl/images/1364/7503/107ce.png) не принадлежит 1 ≤ t ≤ 2.
не принадлежит 1 ≤ t ≤ 2.
x(1)=2*1⁵−2*1+7=7 наименьшее значения функции
x(2)=2*2⁵−2*2+7=64-4+7=67 наибольшее значения функции