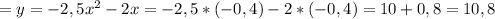Найди координаты вершины параболы y=−2,5x2−2x.
Другие вопросы по теме Алгебра
Популярные вопросы
- Де запалюють вогонь для естафети олімпійського вогню у рік проведення Олімпійських...
2 - Надо из вопросов излечь право и мораль и заполнить таблицу Вопросы: 1. Кто вырабатывает...
3 - В перечне: KClO3, Cl2, HF, CBr4, AgBr– число формул веществ, в которых галогены...
1 - КПД теплового двигателя равен 30%. Какое количество теплоты отдает двигатель холодильнику,...
3 - Есть 15 заданий по теме «Сочетания» и 7 заданий по теме «Размещения». Каким количеством...
1 - 5. Тело, подброшенное вертикально вверх, через 6 с упало на землно. Какой была начальная...
3 - климатические пояса выделяются по режиму воздушных масс.их 4.с учётом двух полушарий...
3 - 1)Пешеход шёл 4 ч со скоростью 5 км/ч, а мотоциклист ехал 2 ч со скоростью 40 км/ч....
1 - что вписать где зеленые точки?...
3 - Сөйлемдерді әрқайсына екі сұрақ қой...
1
Объяснение:
Координаты вершины параболы (графика функции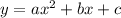 , где а ≠ 0) находятся так:
, где а ≠ 0) находятся так:
(Х; У) =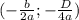 где D - это дискриминант.
где D - это дискриминант. 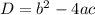
Т.е. Х вершины =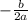
а У вершины =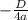
Х вершины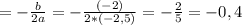
Чтобы найти У вершины, можно и подставить значения Х вершины в данное уравнение функции (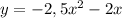 )
)
У вершины