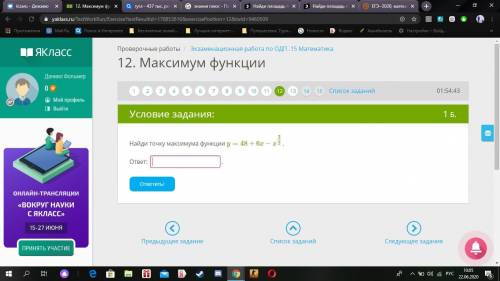
Най­ди­ точку мак­си­му­ма функ­ции

ответ :16

найдём производную, приравняем к нулю и решим уравнение

6-3/2√x=0

6=3/2√x   /* 2/3

4=√x

x=16

Объяснение: Найдем производную и приравняем к нулю, (-3/2√х)+6=0,

√х=4; х=16; при переходе через критич. точку знак производной меняется с плюса на минус.

16

+                           -

   х=16- точка максимума.