1. Алгебра
  2. Най­ди­те зна­че­ние

Най­ди­те зна­че­ние вы­ра­же­ния 90*(-0,1)^4-7*(-0,1)^2-1​

2018kat 2018kat    2   20.05.2021 16:23    0

Ответы
dimaonisko dimaonisko  19.06.2021 16:23

-\frac{1061}{1000} или -1\frac{61}{1000} или -1,061.

Объяснение:

Если в условии выражения нет ошибки, тогда само выражение будет иметь вид:

90*(-0,1)^4-7*(-0,1)^2-1

Для начала "избавимся" от знака "-" под степенью. Для этого стоит вспомнить, что при чётных значениях степеней отрицательного числа, знак меняется на противоположный. К примеру это легко доказать, если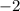 -2 возвести в четвертую степень:

(-2)^{4}=(-2)*(-2)*(-2)*(-2)=4*4=16

Или если число будет в нечётной степени:

(-2)^{3}=(-2)*(-2)*(-2)=4*(-2)=-8

Так и в нашем выражении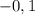 -0,1 возводя в четвёртую и вторую степени, мы избавляемся от знака "минус" перед ними:

90*0,1^4-7*0,1^2-1

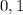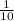Представим 0,1 в виде дроби \frac{1}{10}:

90*(\frac{1}{10}) ^{4} -7*(\frac{1}{10}) ^{2}-1

В данном случае лучше делать прямолинейно и возвести 10 в 4 и во 2 степень:

10^{4} =10*10*10*10=100*100=10000\\(\frac{1}{10}) ^{4} =(\frac{1}{10})*(\frac{1}{10})*(\frac{1}{10})*(\frac{1}{10})=(\frac{1}{100})*(\frac{1}{100})=(\frac{1}{10000})

10^2=10*10=100\\(\frac{1}{10}) ^{2} =(\frac{1}{10})*(\frac{1}{10})=\frac{1}{100}

Вернемся к нашему выражению:

90*\frac{1}{10000} -7*\frac{1}{100}-1

Имеем право 90 и 10000 сократить на 10:

9*\frac{1}{1000} -7*\frac{1}{100}-1

Преобразуем, делая умножение:

\frac{9}{1000} -\frac{7}{100}-1

Теперь следует возведи все числители под один общий знаменатель, таким знаменателем будет 1000:

\frac{9}{1000} -\frac{7}{100}*\frac{10}{10} -1*\frac{1000}{1000}=\frac{9-70-1000}{1000}

Осталось только посчитать разность в числителе:

\frac{9-70-1000}{1000}=\frac{-1061}{1000}=-\frac{1061}{1000}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
aregv aregv  16.12.2020 14:06
6) (x - 3)(x + 2) - 5(x - 4).​...
lphk02 lphk02  16.12.2020 14:07
3a^2-27/18-6a Сократите дробь...
катерринкаа катерринкаа  16.12.2020 14:07
Вычисли y(8), если y(r)= r−5,4....
olgadyra olgadyra  16.12.2020 14:08
Люди с Очень надо, заранее...
MadMax22277 MadMax22277  16.12.2020 14:08
У МЕНЯ КОНТРОЛЬНАЯ 2 ЗАДАНИЯ ОСТАЛОСЬ​...
йцукен56 йцукен56  16.12.2020 14:08
народ задание одно:с Очень надо заранее большое с:...
belos1988 belos1988  19.05.2021 10:09
за 3 булки и 2 конфеты заплатили 22 грививен вопрос сколько стоит одна булочка и одна конфета если 5 булок дороже 4 конфет на 22 гривны ​...
elay0205 elay0205  19.05.2021 10:08
Упростить выражение:Х²+2х+2/у²-9 × у+3/х+1 - х/5у-15​...
ариша037 ариша037  19.05.2021 10:07
Как это решить ? можно подробно? Можно с Photomath...
Прив26789 Прив26789  19.05.2021 10:07
Разложите на множители : x^2y^2 - 9y^2 * 12a^2b + 3ab^2...

Популярные вопросы