1. Алгебра
  2. Натуральное число n

Натуральное число n является произведением 2k простых чисел p1,p2...p2k в каких-то степенях. Может ли\frac{n}{p_{1} } -\frac{n}{p_{2} } + ... - \frac{n}{p_{2k} }=0?

KaterinaReyn KaterinaReyn    1   09.07.2021 19:13    11

Ответы
shulyakovatati shulyakovatati  08.08.2021 20:41

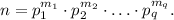Пусть n=p_1^{m_1}\cdot p_2^{m_2}\cdot \ldots \cdot p_q^{m_q}. Обращаю Ваше внимание, что я не собираюсь использовать четность числа различных простых делителей числа p. Обращаю также Ваше внимание, что в условии не сказано, в каком порядке берутся простые делители числа  p. Также я не буду использовать равенство числа положительных и числа отрицательных слагаемых. Итак, можно считать, что нам дана сумма

\frac{n}{p_1}\pm \frac{n}{p_2}\pm \ldots \pm \frac{n}{p;_q}=0; сократив на общие множители, получаем

p_2\cdot p_3\cdot \ldots \cdot p_q\pm p_1\cdot p_3\cdot \ldots \cdot p_q\pm\ldots \pm p_1\cdot p_2\cdot \ldots p_{q-1}=0.

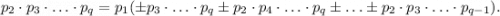
Поэтому p_2\cdot p_3\cdot \ldots \cdot p_q=p_1(\pm p_3\cdot\ldots\cdot p_q\pm p_2\cdot p_4\cdot \ldots \cdot p_q\pm\ldots \pm p_2\cdot p_3\cdot \ldots \cdot p_{q-1}).

Поскольку правая часть делится на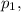 p_1, левая часть  также обязана делиться на 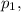p_1,   а это очевидно не так.

Вывод: такое равенство не может  иметь место.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
супер567890 супер567890  02.09.2019 05:50
Турист км за три дня. во второй день он на 10 км меньше, чем в первый день и на на 5 км больше, чем в третий день. сколько км проходил турист каждый день?...
Albina7890 Albina7890  02.09.2019 05:50
Решите уравнение ( x^{2} -6x+4)^2+ ( x^{2} +4x-3)^{2} = (10x-7)^{2}...
Sijjj777 Sijjj777  02.09.2019 05:50
Выполните умножение (4x – 3y) (8x + 6y)....
polycov200412 polycov200412  02.09.2019 05:50
Вопрос, как найти корени биквадратного ривняння. x4-8x2-9=0 за ответ....
роlinka2003 роlinka2003  02.09.2019 05:50
Турист км за три дня. во второй день он на 10 км меньше, чем в первый день. а в третий день 2 раза больше чем во второй. сколько км проходил турист каждый день? найти...
Elv26 Elv26  02.09.2019 05:50
Преобразуйте в многочлен (3x – 7y)^2...
valenkov05 valenkov05  02.09.2019 05:50
Есть два сплава , первый и зкоторых содержит 12%меди , а второй 30%. сколько килограммов каждого слитка надо взять чтобы получить 180 кг сплава , содержащего 25% меди...
annagrits66 annagrits66  02.09.2019 05:50
Прямая y=kx+b проходят через точки a (2; -1) и b (1; -3) .запишите уравнение этой прямой...
igordyatenko igordyatenko  02.09.2019 05:50
Принадлежит ли графику функции у=3х-1 точки а(1; -4) и в(2; 5)?...
FinPinKin FinPinKin  02.09.2019 05:50
Решить (5a³b²)⁴умножить20a²b нужно выражение...

Популярные вопросы