Нашла производную , потом =0 ,получила 3/5 и поставила на функцию и получила 5 ..дальше не знаю что делать
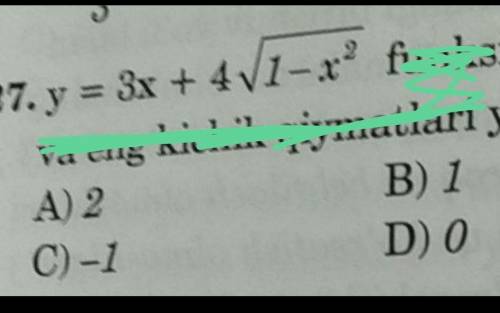
Другие вопросы по теме Алгебра
Популярные вопросы
- 40 слів з м яким знаком.по українській...
1 - Упети было 130 грн,из которых 39 грн он потратил на канцелярские надлежности.какой...
2 - Ограничение расстрат и сохранение качества питьевой воды...
3 - Кто такой михаил сергеевич грушевский? 3 приложения о нём !...
3 - Выполните действия 2,6*4-516: 3+3. -4,6+5*6,6--2*4. 7а-3а+10а...
2 - Схема геополитического положения стран мира...
2 - Придумать простое предложение, в котором нужно поставить, и двоеточие, и дефис,...
2 - Из чисел 19; 42; 66; 85 и 37 выберите два числа , сумма которых делится на 5. сколько...
2 - Прочитайте слова,объясните их правописание.значение неизвестных вам слов найдите...
3 - Составить 6 предложений с причастными и деерпричастными оборотами! с г.д.з предложения...
1
Производная y' = (3х + 4 )' = 3 + 0,5·4 ·(-2x)/
)' = 3 + 0,5·4 ·(-2x)/ = 3 - 4x/
= 3 - 4x/ ;
;
y' = 0 if 3 - 4x/ = 0, (-1 < x < 1) ⇒ 4x = 3
= 0, (-1 < x < 1) ⇒ 4x = 3 ⇔ (обе части
⇔ (обе части
возводим в квадрат при условии x ≥ 0) ⇔ 16х² = 9 - 9х² ⇒ 25х² = 9 ⇒
х₁₂ = ± √9/√25 = ± 3/5. Отрицательный корень откидываем ⇒
х = 3/5 - стационарная точка. При (х = 0,8 > 3/5) y' = 3 - 4*0,8/√0,64 =
3 - 16/3 = - 7/3 < 0 ⇒ х = 3/5 - точка максимума исходной функции, и в ней у принимает наибольшее значение ⇒ Y наиб. = у(3/5) = 9/5 + 4*0,8 = 5; наименьшее значение функции будем искать на концах отрезка [-1; 1]:
y(1) = 3 + 4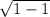 = 3, y(-1) = -3 + 4
= 3, y(-1) = -3 + 4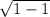 = -3 ⇒ Y наименьшее = y(-1) = -3 ⇒
= -3 ⇒ Y наименьшее = y(-1) = -3 ⇒
Y наиб. + Y наименьшее = -3 + 5 = 2. ответ: А) 2
ответ: A) 5-3=2
Объяснение:
приравняв производную к нулю, находим точку экстремума и
определяем вид экстремума (это точка максимума)
т.к. функция ограниченная, то нужно еще смотреть значения функции на концах отрезка области определения функции...