Напишите все , которыми можно решить уравнение ниже
21+10t-t^2=0

1)  Решение через дискриминант .

2)  Решение с выделения полного квадрата .

3) Решение с теоремы Виета.

Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .

P.S.  Легко подобрать корни по теореме Виета , например, для такого уравнения    .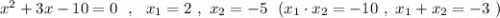

4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения :    .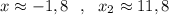

ответ: 3; 7

Объяснение:

1) 21+10t-t²=0

21-10t+t²=0

По Виета t=3; t=7

2) по формуле для приведенного кв. уравнения

t=5±√(25-21)=5±2;  t=3; t=7;

3) по общей формуле корней через дискриминант.  ответ тот же.

(10±√(100-84))/2=(10±√16)/2=(10±4)/2;  t=3; t=7;

4) выделением полного квадрата

(t-5)²=4

It-5I=2; t-5=4; t-5=-4;

⇒t=3; t=7

5) строить не буду, но приведу пример, графический метод решения. правда. в нем есть и минус. не всегда дает точное решение.