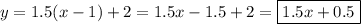Напишите уравнение касательной к графику функции. f(×)= x0=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Аве мария и.с.бахова ,дж.каччини,ф.шуберта сравнить произведения...
1 - Кодиночным причастиям придумайте и запишите пояснительные слова. образец:...
2 - Как этот рассказ читается . dear miss chatter , thank you for letter...
3 - Решить примеры по , подробно 1. (2а - в) во второй степени-(2а-в) * (2а+в)=...
2 - Почему губернатор отговаривал княгиню ехать к мужу ?...
1 - Придумай небольшую о путешествии на любую планету солнечной системы...
2 - 37. варламов, работающий токарем в ао «завод красный путь», принес с...
3 - Доклад по теме годовой жизненный цикл и происхождение земноводных ....
2 - Почему маруся и соня разные детства из рассказа в дурном обществе короленко...
3 - Where go/at 2 pm? правильно составить вопрос...
3
Общий вид уравнения касательной: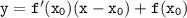
1) Вычислим значение функции в точке x₀ = 1, получим:
Теперь найдем производную функции:
2) Вычислим значение производной в точке x₀ = 1, получим
Уравнение касательной: