1. Алгебра
  2. Напишите общий вид первообразных

Напишите общий вид первообразных для данных функций 1) f(x)=cos^2 x/3 - sin^2 x/3 2) f(x)=sin x/4 * cos x/4 (все действия по порядку )

healarcimbo healarcimbo    3   22.05.2019 23:30    0

Ответы
Диля175 Диля175  01.10.2020 09:31

первообразная- это обратное действие производной, то есть, интеграл.


1)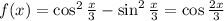 f(x)=\cos^2\frac{x}{3} -\sin^2\frac{x}{3} =\cos\frac{2x}{3} - применен косинус двойного угла.


Первообразная: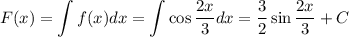 F(x)=\displaystyle \int f(x)dx=\int \cos\frac{2x}{3} dx=\frac{3}{2} \sin\frac{2x}{3} +C


2) Здесь можно решить двумя

F(x)=\displaystyle \int \sin\frac{x}{4} \cos\frac{x}{4} dx=\int \sin \frac{x}{4} d\bigg(\int \cos\frac{x}{4}\bigg)=4\int \sin\frac{x}{4} d\bigg(\sin\frac{x}{4} \bigg)=\\ \\ =4\cdot\frac{\sin^2\frac{x}{4} }{2} +C=2\sin^2\frac{x}{4} +C


В функции f(x) применить синус двойного угла.

F(x)=\displaystyle \int \frac{1}{2}\cdot 2\sin\frac{x}{4} \cos\frac{x}{4} dx=\frac{1}{2}\int\sin\frac{x}{2} dx=-\frac{1}{2}\cdot 2 \cos\frac{x}{2}+C =\\ \\ =-\cos\frac{x}{2} +C


Во втором примере I и оба решения верные, так как при проверке дифференцированием получаются одинаковые результаты. 


(2\sin^2 \frac{x}{4} +C)'=2\cdot 2\sin\frac{x}{4} \cdot (\sin \frac{x}{4} )'=4\sin\frac{x}{4} \cos \frac{x}{4} \cdot(\frac{x}{4} )'=4\sin\frac{x}{4} \cos\frac{x}{4} \cdot \frac{1}{4} =\sin\frac{x}{4} \cos\frac{x}{4}


(-\cos\frac{x}{2}+C)'=\frac{1}{2}\sin\frac{x}{2}=\frac{1}{2}\cdot 2\sin\frac{x}{4}\cos\frac{x}{4}=\sin\frac{x}{4}\cos\frac{x}{4}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Mozgovoi1 Mozgovoi1  18.04.2019 00:20
Розв язати графічно систему рівнянь: 2х+у=1 3х-2у=12...
MiSTiKA23 MiSTiKA23  18.04.2019 00:19
Найти наименьший положительный корень 5sin2x-sin6x+6=0...
nasamar nasamar  18.04.2019 00:19
Найдите значение выражения -у(у-8)+(у+3) при у=1/2 надо выручайте!...
Кюнечка Кюнечка  18.04.2019 00:17
Найти наименьший положительный корень [tex]\frac{ctgx-1}{tgx-1} +\sqrt{2} cosx=0[/tex]...
araratpashayan5 araratpashayan5  18.04.2019 00:14
1-sin5x=-2sin3x найти кол-во корней на [о; π]...
даяна55552 даяна55552  18.04.2019 00:07
Не виконуючи побудов: 1. знайти координати точок перетину графіка функції y=0,3-5 з координатними осями 2. обгрунтуватии, чому графіки функцій y=-12x+23 i y=13x+73 перетинаються,...
hide2 hide2  18.04.2019 01:25
От пристани а к пристани в отправился теплоход с постоянной скоростью первый теплоход ,а через 1 час после этого следом за ним со скоростью , на 1 км в час большей , отправился...
forgalaxynexusp09txz forgalaxynexusp09txz  18.04.2019 01:14
Найдите значение выражения −p(4+ p)+(p−2)(p+2) при p = 3....
Настюшка12305ш384 Настюшка12305ш384  18.04.2019 01:11
Расстояние между пунктами а и в равно 150 км. из пункта а в пункт в выехал легковой автомобиль. одновременно с ним из пункта в в пункт а выехал грузовой автомобиль, скорость...
azko azko  18.04.2019 01:58
Найдите значение выражентя - m(m+2)+(m+3)(m-3) при m=1/3​...

Популярные вопросы