Написать уравнение касательной
y=x^3-3x x0=-1
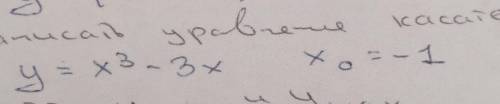
Другие вопросы по теме Алгебра
Популярные вопросы
- будь ласка з твору тореадори з Васюківки написати характеристики героїв...
2 - с этим 189*3. 237*4 59*9. 87 87*3. 294:3 525 :3. 196:7 351:9...
1 - В треугольнике ABC угол С = 90 градусов. катет CB= 9см, а гипотенуза AB =15см....
2 - Соғыс зардаптары 1) Діни2) Әлеуметтік 3) Саяси Өтініш көмектесіңіздерші тез арада...
1 - Алжир Характеристика экономических районов. Крупные города...
1 - Сколько делителей у числа 2×3×5×7...
2 - рассказ Петька на даче Какими кажутся петьке деревня и город что в характере героя...
2 - Develop these ideas (1-4) and use some of the word combinations listed below...
1 - Проверьте текст на грамотность. (нужен текст так чтобы где нужно были запятые...
3 - Капитан Нұрхан Досұлының қылмыскерді құрықтауы...
2
Уравнение касательной к графику функции y = f(x) в точке x₀
имеет вид :