1. Алгебра
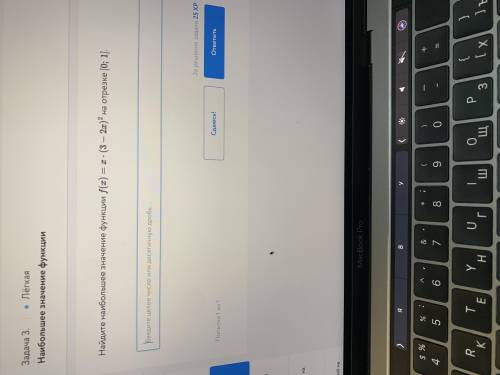
  2. Наибольшее значение функции

Наибольшее значение функции


Наибольшее значение функции

Kristiana132435 Kristiana132435    1   19.10.2021 18:35    0

Ответы
даша33100 даша33100  19.10.2021 18:40

Объяснение:

Непрерывная функция f(x) достигает своего наибольшего значения либо на концах отрезка, либо в точках, где f'(x)=0.

f(x)=x*(3-2x)^2=x*(9-12x+4x^2)=9x-12x^2+4x^3

f'(x)=9-24x+12x^2=12x^2-24x+9;\\f'(x)=0; 12x^2-24x+9=0;\\D=b^2-4ac=(-24)^2-4*12*9=576-432=144;\\x_1=\frac{-b+\sqrt{D}}{2a}=\frac{24+\sqrt{144}}{24}=\frac{24+12}{24}=\frac{36}{24}=1,5

x_2=\frac{-b-\sqrt{D}}{2a}=\frac{24-\sqrt{144}}{24}=\frac{24-12}{24}=\frac{12}{24}=0,5

x_1=1,5 не принадлежит отрезку [0; 1].

Вычислим значение f(x) на концах отрезка и в точке x=0,5.

f(0) = 0;

f(1) = 1;

f(0,5) = 0,5*(3-2*0.5)² = 0.5*2²=0.5*4=2.

Наибольшее значение f(x) равно 2.

ПОКАЗАТЬ ОТВЕТЫ
sorokovilya sorokovilya  19.10.2021 18:40

\boxed{max: f(0,5) = 2}

Объяснение:

f(x) = x(3 - 2x)^{2} ; x\in [0;1]

f(x) = x(3 - 2x)^{2} = x(9 - 12x + 4x^{2} ) = 4x^{3} - 12x^{2} + 9x

f'(x) = (4x^{3} - 12x^{2} + 9x)' = (4x^{3})' - (12x^{2})' + (9x)' = 4(x^{3})' - 12(x^{2})' + 9(x)'=

= 12x^{2} - 24x + 9

f'(x) = 0

12x^{2} - 24x + 9 = 0|:3

4x^{2} - 8x + 3 = 0

D = 64 - 4 * 4 * 3 = 64 - 48 = 16 = 4^{2}

x_{1} = \dfrac{8 + 4}{2 \cdot 4} = \dfrac{12}{8} = 1,5

x_{1} = \dfrac{8 - 4}{2 \cdot 4} = \dfrac{4}{8} = 0,5

При x \in \mathbb R

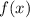Функция f(x) убывает при x \in [0,5;1,5]

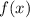Функция f(x) возрастает при x \in (-\infty;0,5] \cup [1,5;+\infty)

При x\in [0;1]

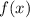Функция f(x) убывает при x \in [0,5;1]

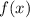Функция f(x) возрастает при x \in [0;0,5]

f(0) = 4 * 0^{2} - 12 * 0^{2} + 9 * 0 = 0

f(1) = 4 * 1^{3} - 12 * 1^{2} + 9 * 1 = 4 - 12 + 9 = 1

max: f(0,5) = 4 * 0,5^{3} - 12 * 0,5^{2} + 9 * 0,5 = 0,5 - 3 + 4,5 = 2

min: f(0) = 0


Наибольшее значение функции
Наибольшее значение функции
Наибольшее значение функции
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
dinadaybert dinadaybert  22.09.2019 11:00
Является ли решение системы неравенств 7 х 9 (х- 5 ) -14. 4х-32 3х...
natilis natilis  22.09.2019 11:00
По ! решите систему уравнений {2x+4y =10 {x-8y=-5 в ответ запишите сумму значение переменных...
Milki0Way0 Milki0Way0  22.09.2019 11:00
Дана арифметическая прогрессия а n в которой а 3 равно 6,9 а 16 равно 26,4 найдите разность прогрессии...
lubovsher1 lubovsher1  22.09.2019 11:00
Найдите значение выражения sin 2a + cos 2a, если a= п/6...
listova listova  22.09.2019 11:00
Разложите на множетели а) а-16в² б) 36y²-(4+5y) ²...
kolya144 kolya144  21.07.2019 03:10
Reshite pobracki (2x-3)^4-23*(2x-3)^2-468=0 otvet: -1,4; -1 nujno imenno !...
Бегимотик002 Бегимотик002  21.07.2019 03:10
Решить уравнение: x^2+1/x^2=x-1/x+2...
qweravq qweravq  21.07.2019 03:10
Как выразить у через х из уравнения 6х-12у+18=0 нужно. завтра сдавать тест. заранее ....
vlad007g vlad007g  21.07.2019 03:10
Найдите значение выражения -2cos60°+sin30°×ctg135°...
nikzarubenko nikzarubenko  21.07.2019 03:10
Докажите нечетность функции y=sin3x-tg2x...

Популярные вопросы