Нахождение производной функции, нужно решить 2 и 4, сам не понимаю как это сделать, заранее
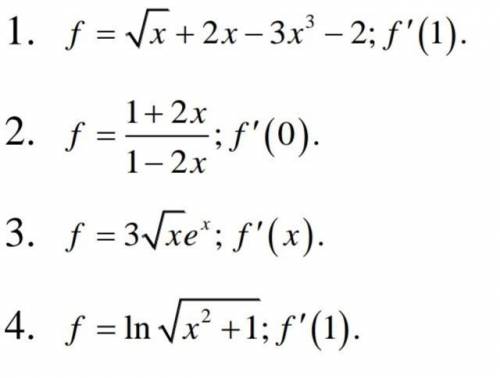
Другие вопросы по теме Алгебра
Популярные вопросы
- Укажите крупнейшие полноводные реки Юго-Западной Азии Тигр и Евфрат Лена и Енисей...
2 - Знайти вираз, який дістанемо розкривши дужки у виразі -5р помножити на (-х+2у-3k)...
2 - Вставьте пропущенные предлоги, частицы и союзы, где это необходимо. Economic...
2 - 1. Розв яжіть квадратне рівняння: а) х2 – 5х + 4 = 0; б) у2 + 9у = 0; в) 2t2...
3 - Через розчин камяної солі пропускають електричний струм. які дії струму можна...
1 - Яку подію можна вважати межею, після якої Українська козацька держава розпалася...
3 - как можно быстрее тороплюсь ...
2 - Силы, которыми удерживаются протоны и нейтроны в ядре...
1 - Составить блок-схему и программу для вычисления площади фигуры (qBasic)...
2 - Найти у/, если: а) у = cos(4х - п); б) у =( 7 - 9х)^14....
3
Объяснение:
2) по формуле производная частного
(u/v)'=(u'v-uv')/v²
(1+2x)/(1-2x)'=[(1+2x)'(1-2x)-(1+2x)(1-2x)']/(1-2x)²=
=[2(1-2x)-(1+2x)(-2)]/(1-2x)²=
=[2(1-2x)+2(1+2x)]/(1-2x)²=
=2[1-2x+1+2x]/(1-2x)²=
=4/(1-2x)²
f'(0)=4/(1-2*0)²=4
4) производная сложной функции (F(g(x))'=F'(g) * g'(x)
а также (lnx)'=1/x ; (√x)'=1/(2√x) ; (x^n)'=nxⁿ⁻¹
f'(x)=(1/√(x²+1)*(1/(2√(x²+1))2x=x/(x²+1)
f'(1)=1/(1²+1)=2
Производную надо скорее знать, чем понимать, то есть с заученными правилами ты без проблем сможешь решить любую задачку на производную. Во вложениях я оставлю некоторые правила дифференцирования и прозводные некоторых элементарных функций.
Но вернемся к нашим баранам. Задача 2.
f=(1+2x)/(1-2x). По правилу производной от частного:
f'=((1+2x)' * (1-2x) - (1-2x)' * (1+2x)) / (1-2x)^2 =
=(2*(1-2x) - (-2)*(1+2x)) / (1-2x)^2 =
= (2-4x+2+4x) / (1-2x)^2 = 4 / (1-2x)^2
Итого f'(0)=4/(1-0)^2 = 4.
Задача 4.
f=ln(sqrt(x^2+1))
По свойству производной от логарифма:
f' = (sqrt(x^2+1))' / sqrt(x^2+1)
По свойству производной от корня (рассмотрим только числитель):
g' = (sqrt(x^2+1))' = ((x^2+1)^(1/2))' = (1/2) * (1/sqrt(x^2+1)) * (x^2+1)'
Ну и оставшаяся производная равна
h' = (x^2+1)' = 2x
Итак, собираем все вместе:
f' = g'/sqrt(x^2+1) = h'/(2*(x^2+1) = x/(x^2+1)
Фух, теперь ищем желанное f'(1):
f'(1)=1/(1+1)=1/2
Ну вот вроде и все, если будут вопросы - пиши, попытаюсь ответить.